
Función inversa
Una función inversa de otra es aquella que realiza el camino contrario. Esto significa que para cada elemento de la imagen, devuelve la preimagen. De esta manera, la imagen de la función original pasa a ser el dominio de la función inversa. Se escribe con el nombre de la función original y un “-1” en el exponente.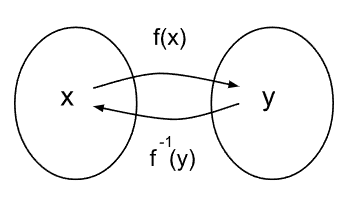
Un ejemplo de una función junto a su inversa lo podemos ver en el siguiente gráfico.
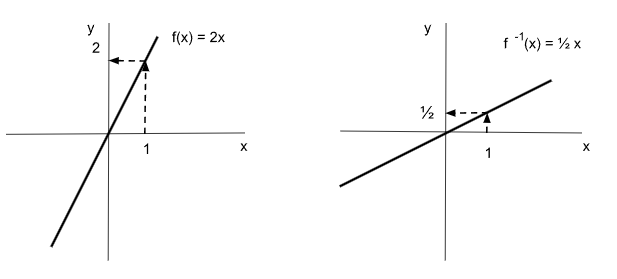
Formalmente podemos expresar:
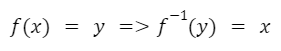
Otra notación usual es utilizar un asterisco en el exponente:
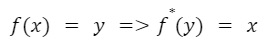
Gráfica de la función inversa
La función inversa es simétrica respecto de la primera diagonal del gráfico de la función original.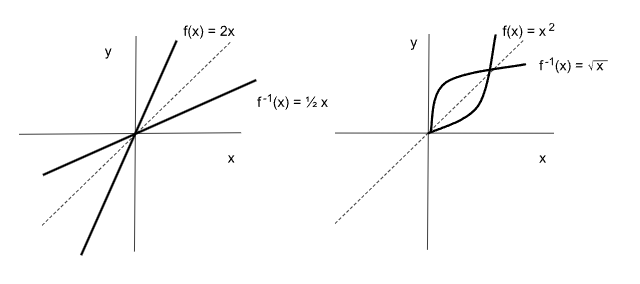
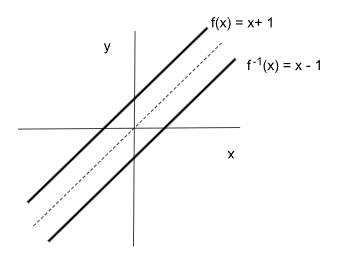
Existencia de la función inversa
Debido a que una función solo puede tener una única imagen para cada valor de su dominio, la función inversa existe si la función original es biyectiva, ya que como mencionamos, los elementos de la imagen pasan a ser los elementos del dominio y viceversa. En el caso que una función no sea biyectiva puede realizarse una restricción de dominio a aquellos valores de su dominio en los cuales la función es biyectiva y obtener la función inversa en esos intervalos.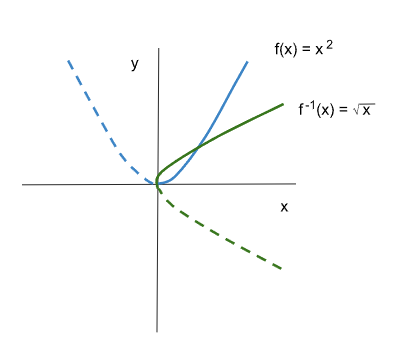
Cómo obtener la función inversa
Para obtener la función inversa debemos seguir los siguientes pasos:- Escribir la función original en la forma y = f(x)
- Despejar la variable “x”
- Intercambiar las variables “x” e “y” entre sí.
En primer lugar escribimos la función en la forma y = f(x).
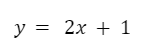
Despejamos la variable “x”.
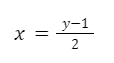
Intercambiamos las variables “x” e “y”.
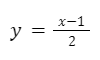
De esta manera nos queda:
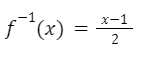
Propiedades de la función inversa
La composición entre una función y su función inversa es igual a la función identidad.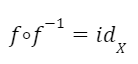
La función inversa de una función inversa es igual a la función original.
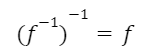
La función inversa de una composición puede distribuirse cambiando el orden de las funciones.
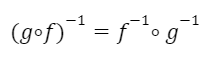
Seguir a funciones de varias variables
Volver a funciones
Volver a home