Clasificación de funciones

Funciones inyectivas

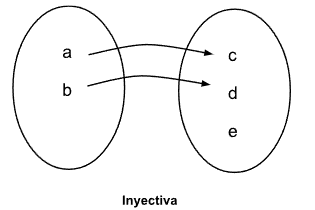
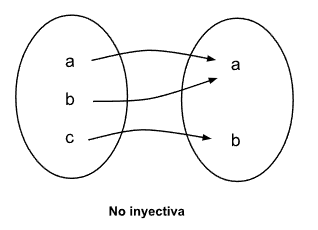
Una función es inyectiva, o también llamada uno a uno, si a diferentes valores de la variable independiente le corresponden diferentes valores de la variable dependiente. Dicho de otra manera, no hay ningún elemento en la imagen que provenga de elementos diferentes del conjunto de salida.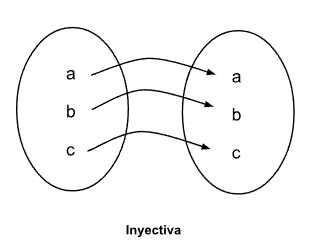

Definición formal

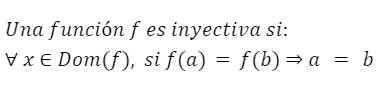
Identificación de funciones inyectivas

Una forma simple de determinar si una función es inyectiva es analizando su gráfica. Si ninguna línea horizontal corta a la función en más de un punto entonces la función es inyectiva.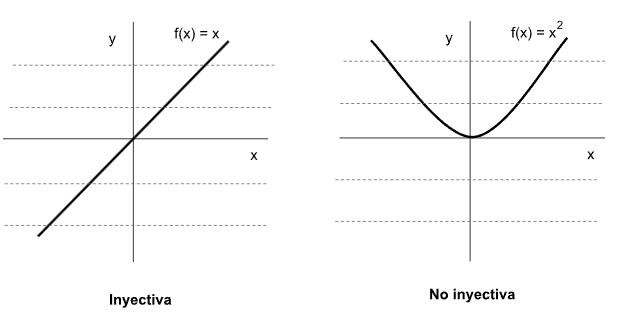



Una forma de comprobar algebraicamente si una función es inyectiva es igualarla a una misma función cambiando el nombre de la variable independiente y verificando que ambas variables sean iguales.

Ejemplo 1

Verificar si la función y = x+1 es inyectiva.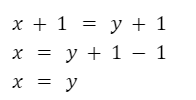



La función es inyectiva.

Ejemplo 2

Verificar si la función y = x² es inyectiva.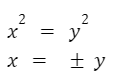



La función no es inyectiva.

Funciones sobreyectivas

Una función es sobreyectiva si todos los elementos del conjunto de llegada provienen de al menos un elemento del conjunto de salida.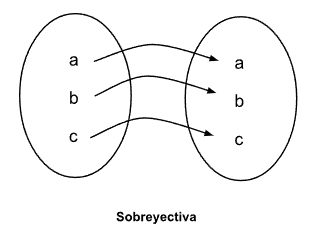

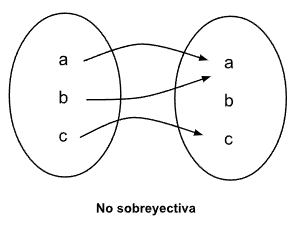
Funciones biyectivas

Una función es biyectiva cuando es inyectiva y sobreyectiva. Dicho de otra manera, una función es biyectiva cuando todos los elementos de la imagen tienen una sola preimagen y no hay ningún elemento del conjunto de llegada que no tenga preimagen.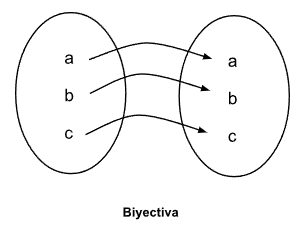








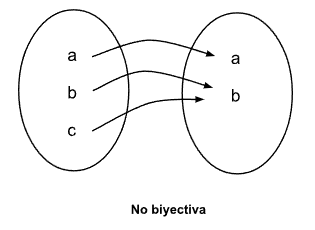
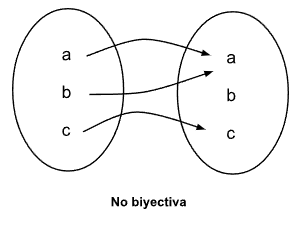
Seguir a función lineal
Volver a funciones
Volver a home