Composición de funciones
La composición de funciones es la aplicación sucesiva de dos o más funciones. Se representa por el operador ∘.Cómo sabemos, una función es una relación entre dos conjuntos que asigna a cada elemento del primer conjunto un único elemento del segundo conjunto. Los elementos del primer conjunto se denominan argumentos de la función y ese conjunto se denomina dominio.
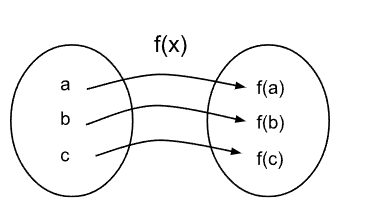
Una segunda función puede recibir como argumento el resultado de haber aplicado la primera función. Dicho de otra manera, la imagen de la primera función es también el dominio de la segunda.
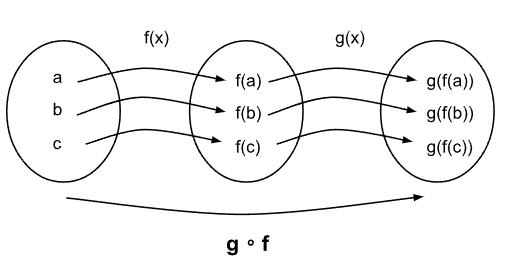
A la función que aplica sucesivamente dos o más funciones de esta manera se la denomina función compuesta. Si se aplica la función “f” y luego se aplica la función “g”, la función compuesta se denomina g∘f. Debemos prestar atención a que se indica primero la segunda función que se aplica. Esto es debido a que cada resultado se obtiene aplicando g(x) al resultado de f(x).
Una función también puede componerse consigo misma. Por ejemplo, f∘f representa la aplicación sucesiva dos veces de la función “f”.
Una función puede estar compuesta por varias funciones. Por ejemplo h∘g∘f representa la composición de tres funciones. En este caso primero se aplica “f”, luego “g” y por último “h”.
Obtener la función compuesta
Dadas dos funciones “f” y “g”, la función compuesta se obtiene reemplazando el argumento de la segunda función por la expresión de la primera.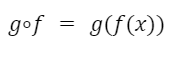
Propiedades de la composición de funciones
La composición de funciones en general no es conmutativa. En casos particulares puede serlo.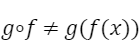
La composición de funciones es una operación asociativa.
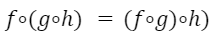
El elemento neutro de la composición de funciones es la función identidad.
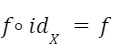
Dominio de una función compuesta
El dominio de una función compuesta está formado por todos los valores que pertenezcan al dominio de la primera función aplicada siempre que la imagen de esos valores pertenezcan al dominio de la segunda función.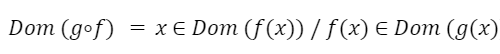
Vamos a verlo más detalladamente. Como sabemos, en la función g∘f de aplica primero f(x) y al resultado se le aplica g(x).
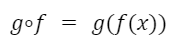
Entonces, los valores “x” que pertenecen al dominio de la función compuesta en primer lugar deben pertenecer al dominio de la función “f”. Luego de aplicar esa función obtenemos f(x). Esos valores deben pertenecer al dominio de la segunda función, en este caso “g”.
Seguir a función inversa
Volver a funciones
Volver a home