Funciones de varias variables
Funciones de una variable
En unidades anteriores estudiamos funciones que tienen una única variable independiente, normalmente representada por la letra “x”. En base al valor de la variable independiente, las funciones le asignan un valor a la variable dependiente “y”. Su definición genérica es la siguiente: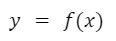
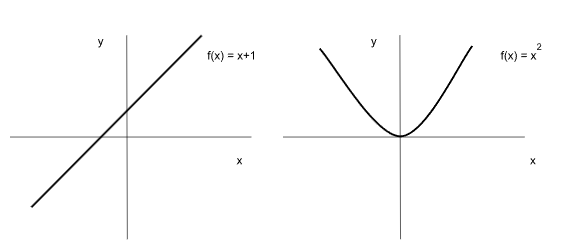
Estas funciones se representan en el plano ya que la función devuelve un valor de “y” para cada valor “x”. Por lo tanto los puntos que forman la función son pares ordenados (x, y) que pueden graficarse.
Funciones de dos variables
En muchas ocasiones, mediante una función se busca obtener un valor que depende de más de una variable independiente. Por ejemplo, una función le puede asignar un valor a una variable dependiente “z” en función de dos variables independientes “x” e “y”.Su definición genérica es:
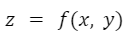
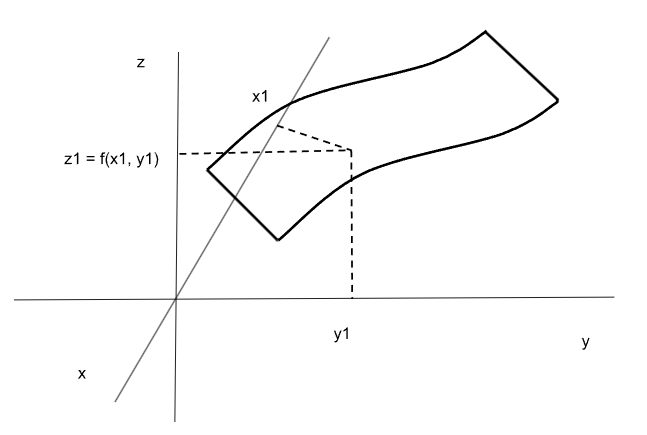
Mientras que las funciones de una variable independiente se representaban en el plano, las funciones de dos variables se representan en el espacio. Es decir que no son rectas o curvas sino superficies. Para cada par (x, y) la función devuelve un valor de “z” y por lo tanto los puntos que forman la función tienen tres coordenadas con la forma (x, y, z).
Funciones de más de dos variables
Hay veces en las que un valor depende de más de dos variables independientes. Para modelar estos casos se utilizan funciones que tienen varias variables independientes aunque no posean un gráfico asociado. Por ejemplo, la siguiente notación representa una función llamada “f” que depende de las variables “x”, “y”, “z”.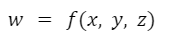
Seguir a par ordenado y tupla
Volver a funciones
Volver a home