
Continuidad de funciones
Una función es continua en un punto X0 cuando se cumplen las siguientes condiciones:- Existe la función en el punto X0 (está definida).
- Existe el límite de la función cuando x tiende a X0 (existen los límites laterales y son iguales).
- El límite de la función cuando “x” tiende a X0 es igual al valor de la función en el punto.
Características de una función continua
En una función continua la gráfica no tiene interrupciones, es decir que puede dibujarse sin levantar el lápiz. Podemos definir la continuidad de una función tanto para un punto como para todo un intervalo.Discontinuidad
Cuando una función es discontinua puede tener una discontinuidad evitable o una discontinuidad no evitable.Discontinuidad evitable
Una función presenta discontinuidad evitable en un punto X0 si existe el límite de la función cuando la variable tiende a X0 (lo que significa que existen los límites laterales y son iguales) pero la función no está definida en ese punto o está definida con un valor distinto al límite cuando “x” tiende a ese punto. Esto se llama discontinuidad evitable debido a que se puede redefinir a la función en ese punto con un valor igual al límite y de esa manera evitar la discontinuidad.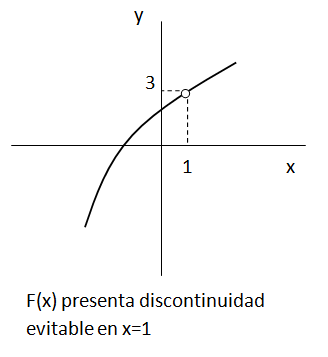
Discontinuidad no evitable
Una función presenta discontinuidad no evitable en un punto X0 cuando no existe el límite de la función en ese punto. Esto significa que no existen los límites laterales o que los límites laterales existen pero son distintos.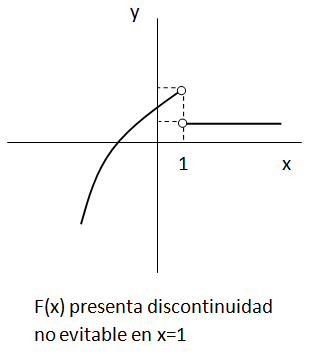
Seguir a límites de dos variables
Volver a límites
Volver a home