Límites de funciones de dos variables

El límite de funciones en dos variables es un concepto muy similar al de una variable, es decir, evalúa a cuánto tiende una función muy cerca de un punto dado.

Sin embargo, en los límites de funciones de una variable nos acercamos al punto a evaluar sobre una única coordenada (en el eje x) ya sea por izquierda o por derecha. En cambio, en los límites de dos variables nos acercamos a un punto de dos coordenadas (x, y) y por lo tanto lo podemos hacer desde varias trayectorias.

Entonces, para calcular un límite de dos variables es necesario asegurarnos que su valor exista cuando nos aproximamos por cualquier trayectoria y además sea igual en todos esos casos.

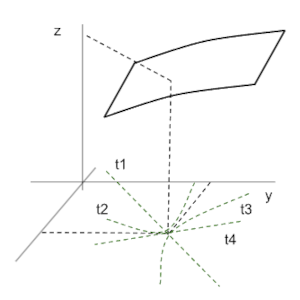
Debemos tener en cuenta que si con dos trayectorias obtenemos resultados diferentes entonces podemos afirmar que el límite no existe, pero para afirmar que el límite existe no es suficiente con obtener dos o más trayectorias con el mismo resultado ya que podría existir otra trayectoria en la que este resultado sea diferente.

Para afirmar que el límite existe es importante conocer el comportamiento de la función.

Trayectorias

Las trayectorias para un límite de dos variables son funciones en el plano, es decir funciones y = f(x) desde las que evaluamos la función.

Algunos ejemplos de trayectorias pueden ser:

• y = 0
• x = 0
• y = x
• y = -x
• y = x2
• y = mx

Ejemplo de límite de dos variables

Calcular el siguiente límite: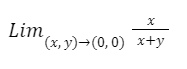



Elegimos la trayectoria y = 0.



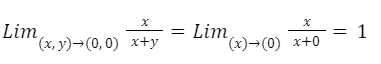
Elegimos la trayectoria y = x.



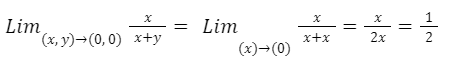
Podemos afirmar que el límite no existe ya que hay dos resultados diferentes.


Seguir a ejercicios resueltos de límites
Volver a límites
Volver a home