Conceptos previos de nomenclatura
Antes de comenzar a estudiar ecuaciones diferenciales es importante saber identificar correctamente las funciones y sus derivadas. En esta sección haremos un breve repaso sobre estos conceptos pero puedes conocer más en detalle estos temas en las secciones correspondientes.Notación de funciones
Una función es una relación entre variables dependientes y variables independientes. En la siguiente expresión vemos una función de ejemplo llamada “f” que tiene como variable independiente a la letra “x”.
Una función también puede expresarse de la forma y = f(x), es decir, indicando cuál es su variable dependiente en lugar del nombre de la función. De esta manera, la función que mencionamos en el ejemplo anterior también puede escribirse como:
Una función puede tener más de una variable independiente. Por ejemplo, la siguiente función “f” tiene dos variables independientes llamadas “x” e “y”.
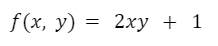
Esta misma función también puede expresarse igualándola a una variable dependiente, por ejemplo “z”. En este caso “z” es igual a f(x, y). Entonces, la función puede escribirse de la siguiente manera:
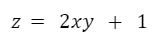
Notación de derivadas
La derivada de una función indica la razón de cambio de la función en un punto dado, es decir la velocidad con la que crece o decrece. Es posible hablar también de una función derivada que es una función que permite calcular la derivada para cada punto.Imaginemos una función genérica:
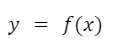
Una de las notaciones de derivadas, denominada notación de Lagrange, expresa las derivadas con un signo prima en la variable dependiente o en el nombre de la función. Por ejemplo:
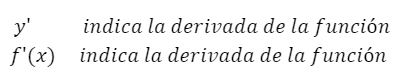
Para derivadas sucesivas se repiten estos signos hasta la tercera derivada o se indican números entre paréntesis en el exponente para derivadas superiores.
En cualquiera de los casos mencionados anteriormente nos referimos a la primera o segunda derivada respecto de la variable independiente.
Otra forma de expresar derivadas, llamada notación de Leibniz, indica explícitamente cuál es el nombre de la variable independiente. Es especialmente importante en funciones de varias variables para indicar respecto de cuál variable se está derivando.
Volver a ecuaciones diferenciales
Volver a home