Definición de ecuaciones diferenciales

Una ecuación diferencial es una ecuación que contiene una función desconocida y derivadas respecto de una o más de sus variables. Dicho de otra manera, es una ecuación que contiene una función y sus derivadas.

También podemos decir que una ecuación diferencial es una igualdad en la que aparecen funciones (o variables dependientes), variables independientes y derivadas de las funciones respecto de las variables independientes.

Las derivadas que aparecen en una ecuación diferencial pueden ser tanto de primer orden como de orden superior. Por ejemplo, puede aparecer también la segunda derivada, la tercera derivada, etc.

Entonces… ¿Qué podemos encontrar en una ecuación diferencial?

• Variables independientes
• Variable dependiente (o función)
• Derivadas de la función respecto de las variables independientes

Ejemplos de ecuaciones diferenciales

Veamos la siguiente ecuación: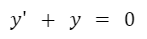



La expresión anterior es una ecuación diferencial. En este ejemplo específico nos indica que la derivada de una función sumada a la función original es igual a cero. Esta ecuación también podría estar planteada con otras notaciones de derivadas.



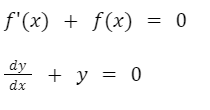
Los siguientes también son ejemplos de ecuaciones diferenciales.



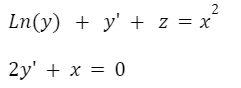
Como mencionamos, en las ecuaciones diferenciales pueden aparecer derivadas de orden superior. Por ejemplo, las siguientes también son ecuaciones diferenciales:



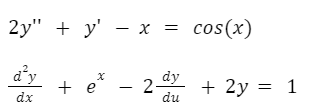
También podemos tener ecuaciones diferenciales con derivadas de varias variables. Por ejemplo, en la siguiente ecuación aparecen derivadas parciales de tres variables independientes.

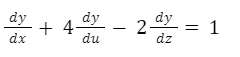
Solución de una ecuación diferencial

La solución de una ecuación diferencial consiste en hallar una función tal que se cumpla la igualdad. Esto quiere decir que la solución no es un número como en el caso de las ecuaciones algebraicas sino una función. Desde ya, esta función podría ser una función constante.

Solución trivial

Si la solución a una ecuación diferencial es una función igual a cero, entonces a esta solución se la denomina solución trivial.

Comprobar la solución

Para comprobar si una función es solución de una ecuación diferencial lo que debemos hacer es reemplazar esa función en la ecuación, calcular sus derivadas cuando sea necesario y luego verificar que se cumpla la igualdad.

Por ejemplo, dada la siguiente ecuación diferencial:



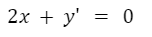
Se desea verificar si la siguiente función es solución:



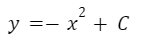
Lo que hacemos es reemplazar la función y obtenemos la siguiente expresión:



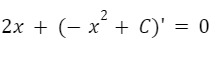
Luego calculamos la derivada:



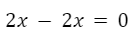
Dado que se cumple la igualdad entonces se verifica que la expresión dada es una solución.


Seguir a clasificación de ecuaciones diferenciales
Volver a ecuaciones diferenciales
Volver a home