Cómo resolver límites

Para resolver límites lo primero que hay que hacer es reemplazar la variable independiente de la función (usualmente “x”) por el valor al cual tiende. Si obtenemos un resultado numérico, ese valor es el resultado del límite.

Si obtenemos una expresión en la que se divide un valor numérico por cero, el resultado del límite es ∞ ya que, si bien no se puede dividir por cero, sabemos que si tomamos valores cada vez más pequeños y evaluamos la función en esos valores obtendremos números cada vez más grandes.

Es posible que obtengamos muchos otros resultados que podemos interpretar, tales como un número dividido por infinito, cuyo resultado sabemos que es cero, ya que si dividimos un valor por números cada vez más grandes el resultado será cada vez menor.

Al resolver límites debemos evaluar que pasa si nos acercamos por derecha o si nos acercamos por izquierda (límites laterales). Si ambos resultados son diferentes entonces el límite no existe.

También es posible que obtengamos una indeterminación, es decir un resultado que no podemos interpretar. Las posibles indeterminaciones son las siguientes:

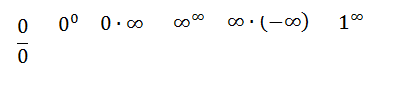
¿Cómo resolver las indeterminaciones?

Si obtenemos una indeterminación lo que debemos realizar es algún cambio en la forma del límite, sin modificar su valor, de tal forma que desaparezca la indeterminación.

Algunas de las posibles formas de salvar una indeterminación son:

• Dividir el numerador por el denominador
• Factorizar y simplificar
• Multiplicar y dividir por el conjugado
• Racionalizar

Seguir a continuidad de funciones
Volver a límites
Volver a home