
Suma y resta de vectores
Para coordenadas cartesianas
La suma y resta de vectores se realiza sumando o restando cada una de las componentes de cada uno y da como resultado otro vector.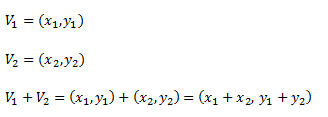
Para sumar dos vectores, los mismos tienen que tener la misma cantidad de componentes.
Ejemplo
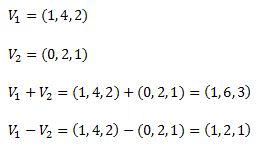
Gráficamente la suma y resta de vectores se puede realizar por el método del paralelogramo, es decir trazar sobre cada vector una recta paralela al otro formando un paralelogramo, cuya diagonal es la suma.
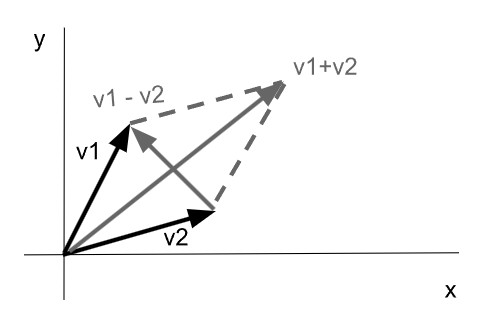
Para coordenadas polares
Ver suma de fuerzas.Propiedades
La suma de vectores es conmutativa.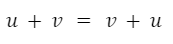
La resta de vectores en general no es conmutativa.
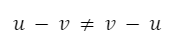
La suma de vectores es asociativa.
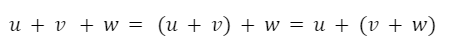
El elemento neutro de la suma y de la resta es el vector nulo.
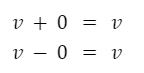
Seguir a producto de un escalar por un vector
Volver a vectores
Volver a home