
Producto de un escalar por un vector
El producto de un escalar por un vector da por resultado otro vector, con la misma dirección que el primero. Al hacer la multiplicación, el escalar cambia el módulo del vector (gráficamente el largo) y en caso de ser negativo cambia también el sentido. La dirección del vector resultado es siempre la misma que la del vector original.Matemáticamente se realiza multiplicando al escalar por cada una de las componentes del vector.
Si por ejemplo el vector V tiene 2 coordenadas:
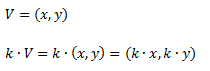
Ejemplo
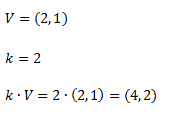
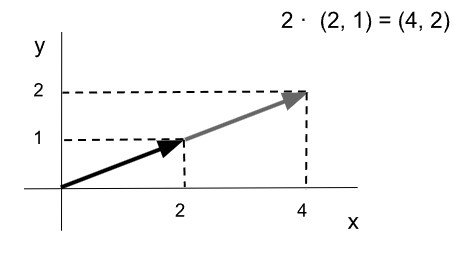
Ejemplo
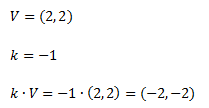
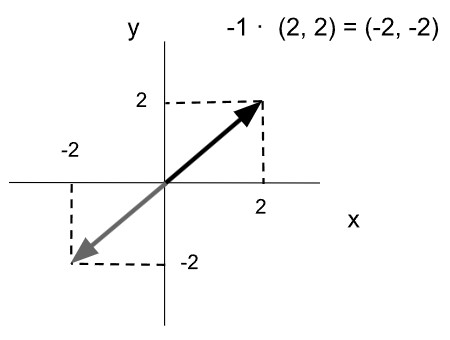
Si los vectores son de más de dos coordenadas se realiza lo mismo por cada una de ellas.
Propiedades del producto de un escalar por un vector
Es conmutativo.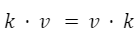
Es distributivo con respecto a la suma de vectores.
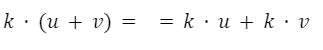
Es distributivo respecto a la suma de escalares.
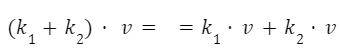
El número uno es el elemento neutro.
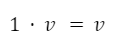
El número cero es el elemento absorbente.
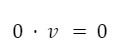
Si se multiplica un vector por “-1” el resultado es un vector con la misma longitud y la misma dirección pero de sentido contrario.
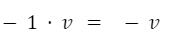
El módulo del producto de un escalar por un vector es igual al módulo del escalar por el módulo del vector.
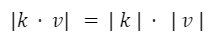
Producto escalar
Volver a vectores
Volver a home