Método de variables separables
El método de variables separables se utiliza cuando la ecuación diferencial puede escribirse de tal forma que las variables dependiente e independiente aparezcan una a cada lado de la igualdad. Formalmente se dice que una ecuación es de variables separables cuando puede escribirse de la forma: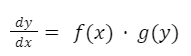
Observemos que en la expresión anterior “dx” puede pasarse multiplicando hacia la derecha mientras que g(y) puede pasarse dividiendo hacia la izquierda y de esta manera quedan las variables separadas. De forma general, podemos identificar una ecuación de variables separables cuando la derivada de la función está igualada a un producto o cociente de funciones de “x” e “y”.
Recordemos que si en una ecuación aparece la derivada de una función con el signo prima, la podemos reemplazar como un cociente de dos diferenciales:
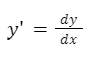
Ejemplos de ecuaciones de variables separables
Vamos a ver algunos casos de ecuaciones de variables separables y cómo podemos reescribir las ecuaciones. Este es el primer paso para luego encontrar una solución.Veamos la siguiente ecuación:
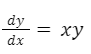
Es posible pasar el “dx” multiplicando y la “x” dividiendo y por lo tanto tener separadas las variables.
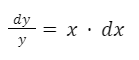
Analicemos ahora la siguiente ecuación:
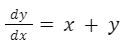
Como vemos, no es posible separar las variables a cada lado, por lo que no es una ecuación diferencial de variables separables.
Pasos para resolver una ecuación de variables separables:
- Separar las variables a uno y otro lado de la igualdad.
- Integrar ambos lados de la ecuación, agregando las constantes de integración.
- Despejar la variable dependiente “y”, de tal forma de que nos quede igualada a una función de x.
Ejemplo de resolución de ecuaciones por este método
Veamos la siguiente ecuación: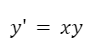
En primer lugar escribimos su derivada según la notación de Leibniz, es decir como un cociente de dos diferenciales.
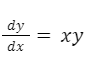
Separamos las variables:
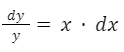
Integramos a ambos lados:
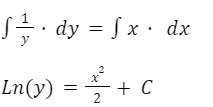
Despejamos y:
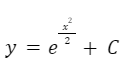
Seguir a ecuaciones diferenciales exactas
Volver a ecuaciones diferenciales
Volver a home