Ecuaciones diferenciales exactas

Dada una ecuación diferencial con la forma: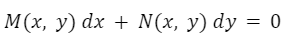



Se dice que exacta si existe una función “F”, llamada función potencial, tal que:



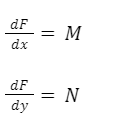
Dicho de otra manera, las derivadas parciales de “F” respecto a cada una de las variables son iguales a las funciones M y N. Estas derivadas son iguales entre sí. Esto también es equivalente a decir que la derivada total de “F” coincide con la ecuación diferencial.

La solución de una ecuación diferencial exacta se obtiene igualando la función potencial a una constante de integración, es decir mediante la siguiente expresión:

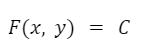
Solución de ecuaciones diferenciales exactas

1. Comprobar que la ecuación diferencial sea exacta derivando “M” y “N” respecto de la variable que no aparece en su diferencial y verificando que ambas derivadas sean iguales.
2. Hallar la función potencial F(x, y), integrando “M” o “N” con respecto a la variable que aparece en su diferencial. Al integrar, en lugar de sumar una constante de integración “C” sumamos una función respecto de la variable que consideramos constante al calcular esa integral, por ejemplo g(y) o h(x).
3. Hallar la función constante g(y) o h(x). Para ello por un lado derivamos F(x, y) con respecto a la variable de nuestra función constante, escribimos “N” o “M” según corresponda e igualamos ambas expresiones.
4. Despejar “y”, obteniendo de esta manera la función solución.

Ejemplo

Obtener la solución a la siguiente ecuación diferencial: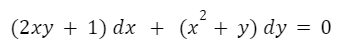



Planteamos la ecuación diferencial como una suma de dos funciones:



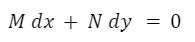
Calculamos las derivadas parciales:



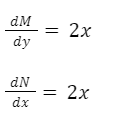
Como las derivadas parciales son iguales entonces la ecuación diferencial es exacta.

Para hallar “F” integramos cualquiera de las dos funciones (M o N) pero al calcular la integral en lugar de sumar una constante “C” sumamos una función constante respecto de la variable dependiente, en nuestro caso g(y) ya que nuestra variable independiente es “x”.



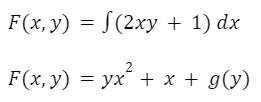
Ahora debemos hallar la función constante g(y). Derivamos F(x, y) con respecto a “y”:



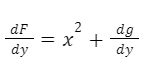
Escribimos la función “N”:



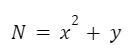
Igualamos ambas expresiones:



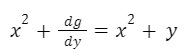
Simplificamos:



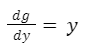
Despejamos la derivada de “g” de la expresión anterior:



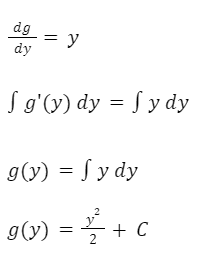
Reemplazamos g(y) en la función potencial hallada:



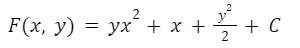
Hallamos la solución a la ecuación diferencial igualando la función potencial a una constante “C”.




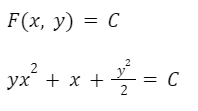
Seguir a ecuaciones diferenciales con valor inicial
Volver a ecuaciones diferenciales
Volver a home