Función logarítmica
La función logarítmica es aquella que tiene la forma: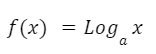
En donde “a” es un número constante y “x” es la variable independiente.
La función logarítmica es la función inversa de la función exponencial.
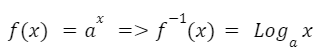
Al igual que la función exponencial tiene un comportamiento diferente para valores de “a” mayores que uno y para valores de “a” comprendidos entre cero y uno.
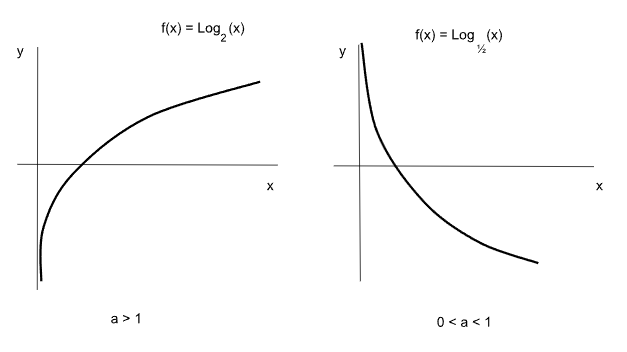
La función logarítmica que tenga la forma Log a (x) siempre corta al eje “x” en el valor “1”, independientemente del valor de “a”. Esto se debe a que cualquier base del logaritmo elevada a cero da uno.
Sin embargo, hay ciertos parámetros que pueden aparecer en la función logarítmica básica, modificando entre otras cosas la intersección con el eje “x”.
Parámetros de la función logarítmica
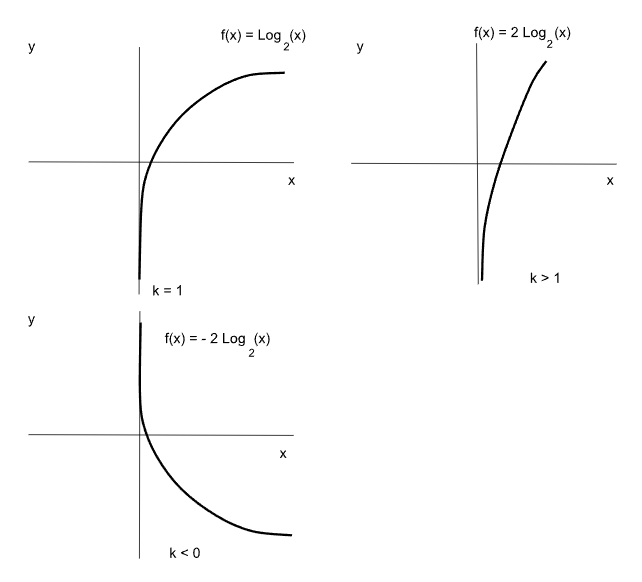
Un parámetro constante “k” que multiplique a la función logarítmica produce una expansión o contracción de la misma. Si “k” es un valor negativo la función es decreciente.El valor de este parámetro no modifica el punto de corte con el eje “x”.
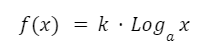
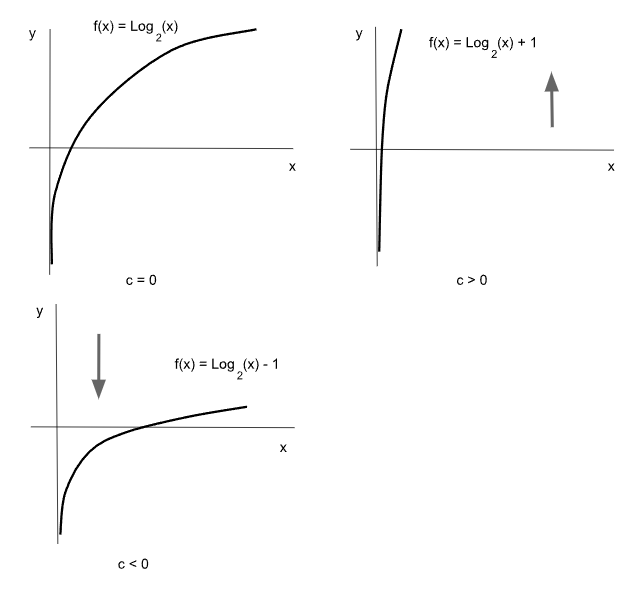
Un parámetro “c” sumado a la función logarítmica produce un corrimiento hacia arriba si es positivo y hacia abajo si es negativo.
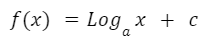
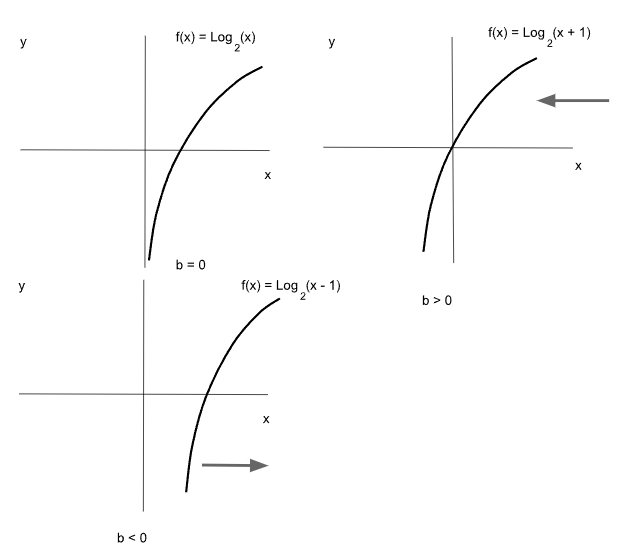
Una constante sumando o restando a la variable independiente produce un corrimiento horizontal. Si el valor es positivo el corrimiento es hacia la izquierda mientras que si es negativo el corrimiento es hacia la derecha.
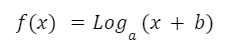
Propiedades de la función logarítmica
- La función logarítmica es la inversa de la función exponencial.
- La función logarítmica es inyectiva, sobreyectiva y biyectiva.
- El dominio son todos los números reales positivos.
- La imagen son todos los números reales.
- Si la base fuese igual a uno se trataría de una función constante.
Volver a funciones
Volver a home