Función exponencial
La función exponencial es aquella que tiene la forma: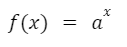
En esta expresión “a” es una constante positiva y distinta de uno mientras que “x” es la variable independiente. Una de las principales características de una función exponencial es que la variable independiente se encuentra en el exponente.
La función exponencial tiene dos comportamientos diferentes, según el valor de la base “a”. Si “a” es mayor que uno la función es creciente, mientras que si “a” se encuentra entre cero y uno la función es decreciente.
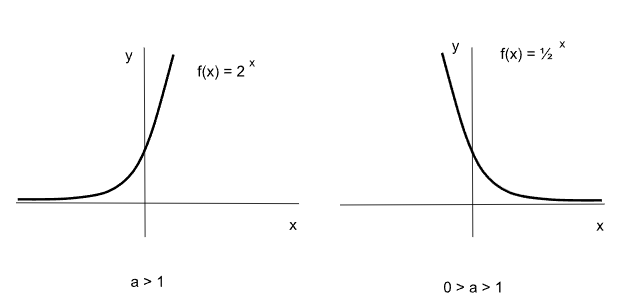
La función exponencial de la forma ax corta siempre al eje “y” en 1, independientemente del valor de “a”. Esto se debe a que cualquier número elevado a cero da como resultado uno. Sin embargo hay ciertos parámetros que puede tener la función y que pueden modificar, entre otras cosas, el lugar en el que la gráfica corta al eje “y”.
Parámetros que modifican a la función exponencial
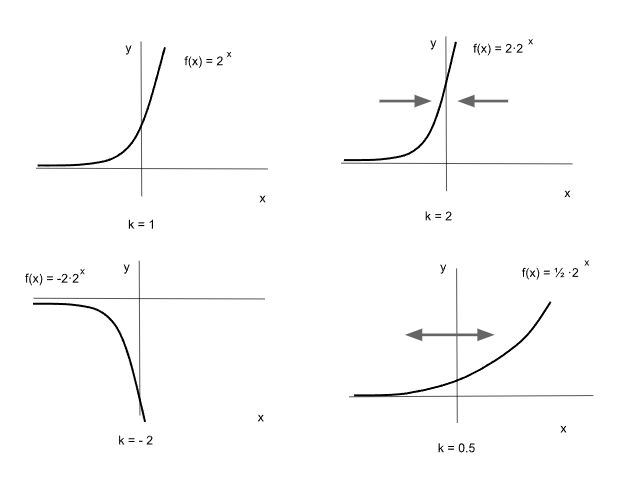
Un coeficiente que multiplica a la base produce una expansión o contracción de la función exponencial. El valor de “k” coincide con el punto de corte del eje “y”. Si el valor de “k” es negativo la función devuelve valores negativos.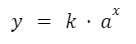
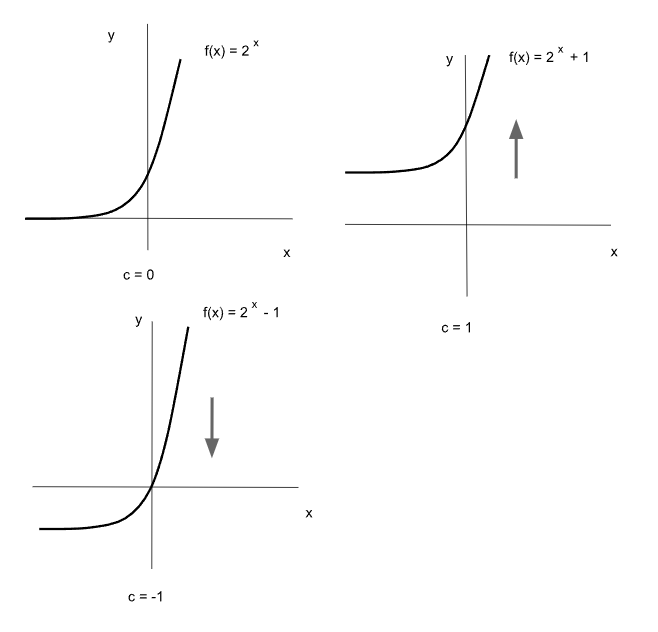
Una constante “c” positiva sumada a la función exponencial produce un corrimiento hacia arriba, mientras que una constante negativa lo hace hacia abajo.
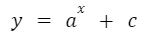
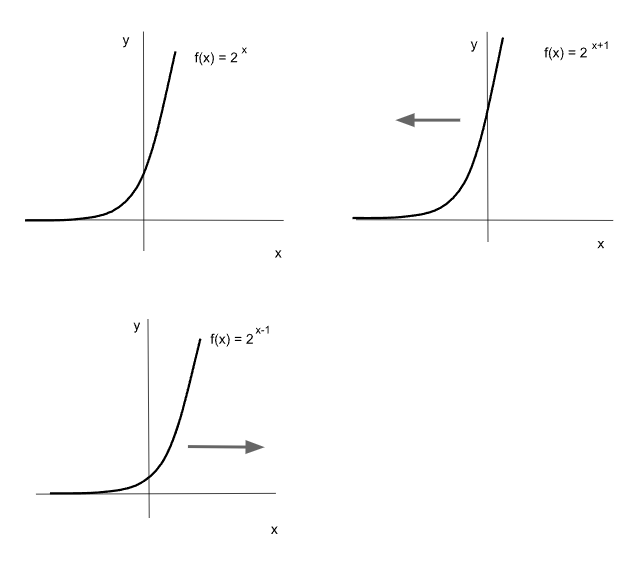
Un valor constante que sume o reste en el exponente produce un corrimiento horizontal de la gráfica. Esto influye también en el punto de corte del eje “y”. Un valor positivo produce un corrimiento hacia la izquierda mientras que un valor negativo lo hace hacia la derecha.
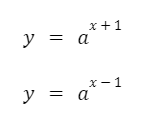
¿Qué pasa si el exponente es negativo?
Por propiedades de la potencia, sabemos que un exponente negativo significa que la base se invierte.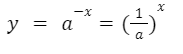
Propiedades de la función exponencial
- La función exponencial es inyectiva, sobreyectiva y biyectiva.
- El dominio de la función exponencial está formado por el conjunto de los números reales.
- La imagen de la función exponencial está formada por el conjunto de los números reales. Si no hay un corrimiento mediante un parámetro, la imagen son todos los números reales positivos.
- Si la base fuese igual a uno, se trataría de una función constante y no exponencial.
Número e
El número “e” es un número irracional de gran importancia dentro de las matemáticas. Es llamado también número de Euler. Se utiliza en variadas aplicaciones, muchas veces relacionado a funciones exponenciales y logarítmicas. El valor de “e” es aproximadamente 2,718 y tiene infinitos decimales.Este número surge de sumar un número “n” de veces el siguiente término:
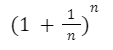
Es decir que nos queda una expresión como la siguiente:
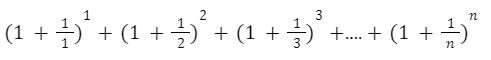
Cuántos más términos sumemos más decimales obtendremos del número “e”.
Crecimiento exponencial
La función exponencial es muy utilizada para modelar situaciones relacionadas con crecimiento acumulado. Por ejemplo la población de una ciudad o de una colonia de microorganismos que aumenta a un determinado porcentaje por cada período.Esto se calcula mediante la siguiente expresión:
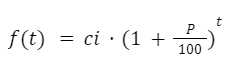
f(t) = Cantidad luego de “t” períodos.
ci = Cantidad inicial.
P= Tasa de aumento en porcentaje.
t = Número de períodos.
Si directamente tenemos expresada la tasa en tanto por uno podemos utilizar la siguiente expresión:
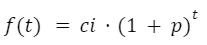
f(t) = Cantidad luego de “t” períodos.
ci = Cantidad inicial.
p= Tasa de aumento en tanto por uno.
t = Número de períodos.
Funciones exponenciales notables
- Si la base es 10 la función se denomina función exponencial decimal.
- Si la base es el número “e” la función se denomina función exponencial natural.
Seguir a función logarítmica
Volver a funciones
Volver a home