
Ejercicios de impedancia equivalente
Ejercicio 1
Hallar la impedancia equivalente del siguiente circuito serie sabiendo que funciona a una frecuencia de 200 Hz.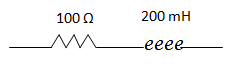
Solución
Reemplazamos los componentes por impedancias para luego calcular el valor de la impedancia total equivalente.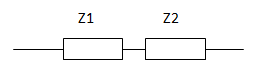
Calculamos la velocidad angular:
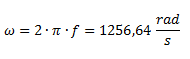
A continuación calculamos el valor de cada impedancia. La impedancia Z1, por ser resistiva pura, no tiene parte imaginaria y su parte real es igual al valor de la resistencia.
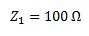
Para calcular la impedancia Z2 primero hallamos la reactancia inductiva.
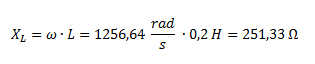
La impedancia Z2, por ser inductiva pura, no tiene parte real y solamente está formada por la reactancia inductiva en su parte imaginaria.
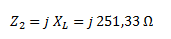
Por tratarse de una asociación en serie, la impedancia total es igual a la suma en forma compleja de las impedancias individuales.
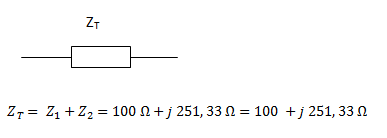
Ejercicio 2
Hallar la impedancia equivalente del siguiente circuito serie sabiendo que funciona a una frecuencia de 200 Hz.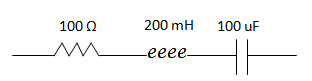
Solución
Reemplazamos los componentes por impedancias para luego calcular el valor de la impedancia total equivalente.
Hallamos la velocidad angular:
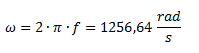
A continuación calculamos el valor de cada impedancia. La impedancia Z1 no tiene parte imaginaria y su parte real es igual al valor de la resistencia.
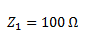
Para calcular la impedancia Z2 primero hallamos la reactancia inductiva.
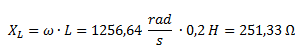
La impedancia Z2 no tiene parte real y solamente está formada por la reactancia inductiva en su parte imaginaria.
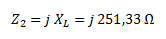
Para calcular Z3 hallamos primero la reactancia capacitiva.
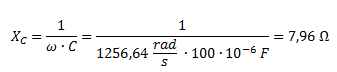
La impedancia Z3 no tiene parte real y por ser capacitiva está formada por la reactancia cambiada de signo.
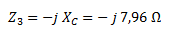
Por tratarse de una asociación en serie, la impedancia total es igual a la suma en forma compleja de las impedancias individuales.
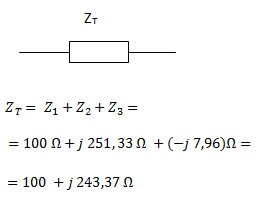
Ejercicio 3
Hallar la impedancia equivalente del siguiente circuito sabiendo que la frecuencia a la cual funciona es de 60 Hz.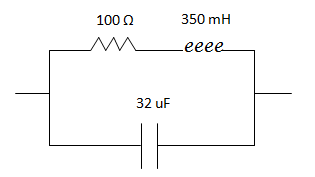
Solución
Para resolver este tipo de circuitos reemplazamos por impedancias a cada uno de los componentes y luego las asociamos para obtener la impedancia total.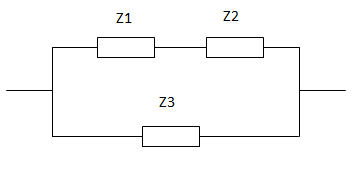
Calculamos primero la velocidad angular a partir de la frecuencia:
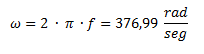
Luego hallamos el valor de cada impedancia.
La impedancia de la resistencia no tiene parte imaginaria y su parte real es igual al valor de la resistencia, por lo tanto nos queda de la siguiente manera:
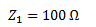
Calculamos la reactancia del inductor:
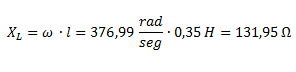
La impedancia del inductor (Z2) no tiene parte real y solo está formada por la reactancia inductiva, por lo tanto nos queda:
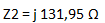
Calculamos la reactancia del capacitor:
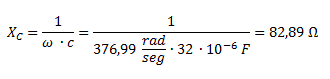
La impedancia del capacitor (Z3) no tiene parte real y solo está formada por la reactancia capacitiva con signo negativo.
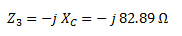
El circuito formado por impedancias nos queda de la siguiente forma:
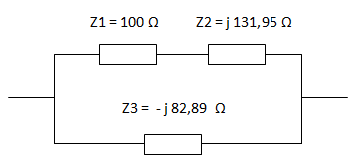
Ahora resolvemos la asociación tal como si se tratara de resistencias, con la diferencia de que las operaciones se realizan con números complejos.
Calculamos la primera impedancia equivalente asociando en serie Z1 con Z2. Debido a que están en serie, la impedancia total es la suma de los dos números en forma compleja.
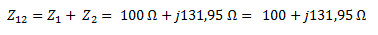
Nos queda el siguiente circuito equivalente:
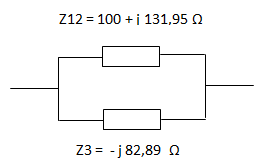
Calculamos la asociación en paralelo de Z12 con Z3. Cómo solo son dos impedancias podemos utilizar la fórmula simplificada.
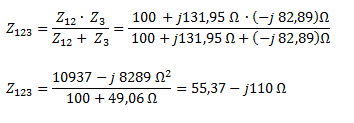
Debido a que nos quedó una sola impedancia, Z123 ya es la impedancia total.
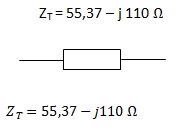
Ejercicio 4
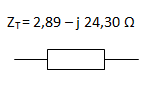
Calcular la impedancia equivalente del siguiente circuito, sabiendo que su frecuencia de funcionamiento es de 60 Hz.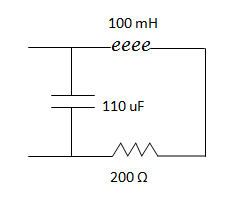
Reemplazamos todos los componentes por impedancias.
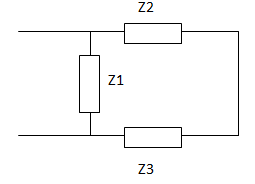
Calculamos la velocidad angular para luego hallar las reactancias:
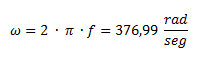
Calculamos la reactancia del capacitor:
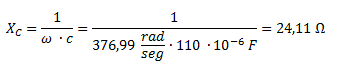
Calculamos Z1 que es la impedancia correspondiente al capacitor. La misma no tiene parte real y solo está formada por la reactancia capacitiva con signo negativo.
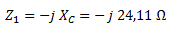
Calculamos la reactancia del inductor:
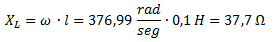
Calculamos Z2 que es la impedancia del inductor. Como solo está formada por la reactancia inductiva, nos queda:
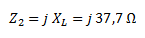
Calculamos la impedancia de la resistencia. No tiene parte imaginaria y su valor es igual al de la resistencia.
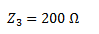
El circuito de impedancias nos queda tal como se indica a continuación.
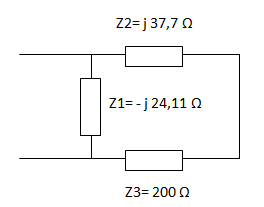
Planteamos la asociación en serie de las impedancias Z2 y Z3.
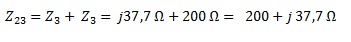
Nos queda el siguiente circuito:
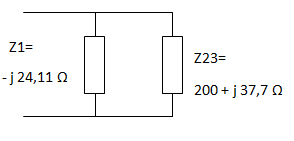
Planteamos la asociación en paralelo de Z1 con Z23. Utilizamos la fórmula simplificada ya que se trata de dos impedancias.
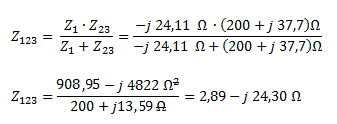
Como nos queda una sola impedancia equivalente, ésta ya es la impedancia total.
Seguir a ejercicios de circuitos RLC
Volver a ejercicios de corriente alterna
Volver a home