Ejercicios de circuitos RLC
Ejercicio 1
Hallar la corriente total que circula por el siguiente circuito. Expresarla con una función coseno.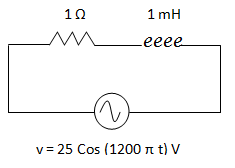
Solución
Para resolver este tipo de circuitos, primero reemplazamos cada componente por su impedancia y calculamos la impedancia total. Luego aplicamos la ley de Ohm, tal como si se tratase de un ejercicio de corriente continua, pero realizando los cálculos con números complejos.Reemplazando por impedancias nos queda un circuito con la siguiente forma:
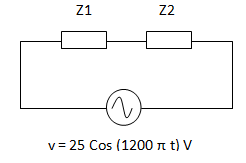
Obtenemos primero la velocidad angular de la fuente a partir de su expresión de tensión.
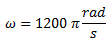
La impedancia de la resistencia es igual a su valor y no tiene parte imaginaria.
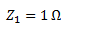
Para calcular Z2 hallamos primero la reactancia inductiva.
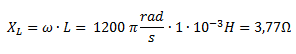
Z2 no tiene parte real y solo está formada por la reactancia inductiva en su parte imaginaria.
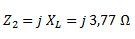
Calculamos Z12 como la asociación en serie de Z1 y Z2. Debido a que no hay otras impedancias, ésta ya es la impedancia total.
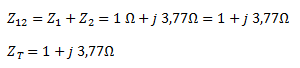
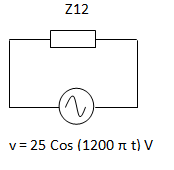
Convertimos la tensión de la fuente a forma fasorial. Como luego debemos obtener una expresión en función del tiempo, utilizamos directamente el valor máximo de tensión como módulo del fasor. Debido a que no hay ángulo de fase, el ángulo del fasor es 0°.
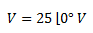
Pasamos la impedancia a forma polar.
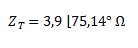
Planteamos la ley de Ohm.
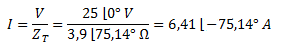
Escribimos la corriente con una función coseno a partir del fasor de corriente hallado.
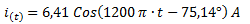
Ejercicio 2
Hallar la corriente que circula y expresarla con una función coseno.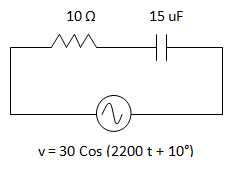
Solución
Reemplazamos todos los componentes por impedancias.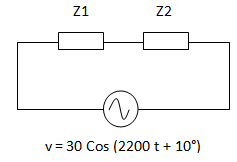
Obtenemos primero la velocidad angular de la fuente a partir de su expresión de tensión.
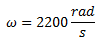
La impedancia de la resistencia es igual a su valor y no tiene parte imaginaria.
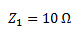
Para calcular Z2 hallamos primero la reactancia capacitiva.
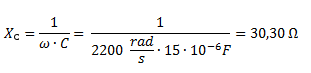
Z2 no tiene parte real y solo está formada por la reactancia capacitiva cambiada de signo en su parte imaginaria.
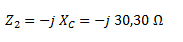
Calculamos Z12 como la asociación en serie de Z1 y Z2. Debido a que no hay otras impedancias, ésta ya es la impedancia total.
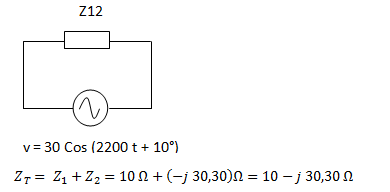
Convertimos la tensión de la fuente a forma fasorial. Utilizamos el valor máximo de tensión como módulo del fasor.
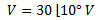
Convertimos la impedancia a forma polar.
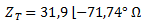
Planteamos la ley de Ohm para corriente alterna.
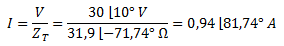
Escribimos la corriente con una función coseno a partir del fasor de corriente hallado.
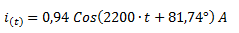
Ejercicio 3
Hallar la expresión de corriente en función del tiempo para el siguiente circuito.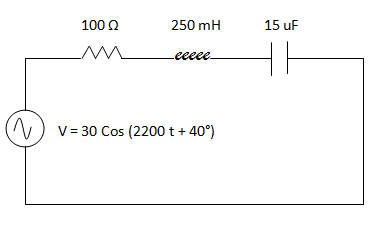
Solución
Reemplazamos cada uno de los componentes por una impedancia equivalente.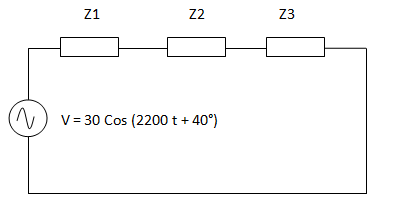
Obtenemos la velocidad angular desde la expresión de tensión.
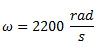
Obtenemos la impedancia Z1. Tiene solamente parte real ya que se trata de una resistencia.
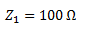
Calculamos la reactancia inductiva y luego la impedancia Z2, que es igual al valor de la reactancia en la parte imaginaria.
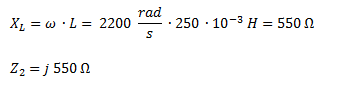
Calculamos la reactancia capacitiva y luego la impedancia Z3, que es igual al valor de la reactancia en la parte imaginaria y con signo negativo.
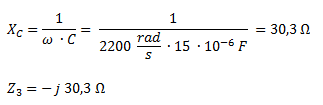
Calculamos la impedancia total. Como se trata de una asociación en serie, sumamos los valores de cada una de las impedancias en forma compleja.
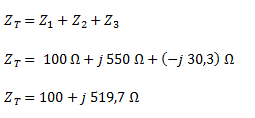
Transformamos la impedancia y la tensión de la fuente a expresiones fasoriales. En el caso de la tensión utilizamos el valor máximo ya que luego debemos expresar nuevamente la señal en función del tiempo.
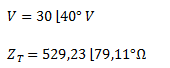
Aplicamos la ley de Ohm para corriente alterna y obtenemos la corriente en forma fasorial.
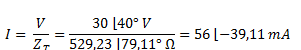
Convertimos el resultado a una expresión en función del tiempo.
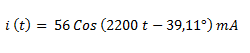
Seguir a ejercicios de factor de potencia
Volver a ejercicios de corriente alterna
Volver a home