Ejercicios de factor de potencia
Ejercicio 1
Una instalación consume una potencia activa de 5,2 kW y una potencia reactiva de 1,1 kVAR en atraso.Calcular el ángulo de desfasaje y el factor de potencia.
Solución
Sabemos que la corriente se encuentra en atraso, por lo tanto la potencia reactiva es del tipo inductiva.El triángulo de potencias es similar al siguiente:
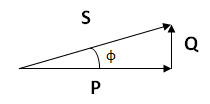
Calculamos primero la potencia aparente (S). Debido a que se trata de la hipotenusa de un triángulo aplicamos el teorema de Pitágoras.
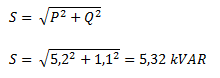
El factor de potencia (que es el coseno del ángulo) lo calculamos como la potencia activa sobre la potencia aparente.
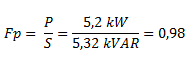
El ángulo lo calculamos a través de la función inversa del coseno.
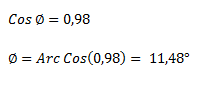
Ejercicio 2
Una instalación consume 3,5 kW de potencia activa con un factor de potencia de 0,8.Calcular la potencia reactiva y la potencia aparente.
Solución
Sabemos que el factor de potencia es igual al coseno del ángulo Φ, por lo tanto podemos hallar el ángulo a través de la función inversa del coseno.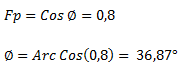
El triángulo de potencias nos queda con la siguiente forma:
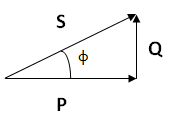
Tanto la potencia reactiva como la potencia aparente la podemos calcular por trigonometría.
Para la potencia reactiva plantemos la siguiente relación:
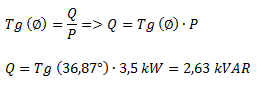
Para la potencia aparente planteamos la siguiente relación:
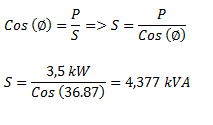
Seguir a ejercicios de corrección del factor de potencia
Volver a ejercicios de corriente alterna
Volver a home