
Ejercicios de corrección del factor de potencia
Ejercicio 1
Una instalación de 220 voltios y 60 Hz consume una potencia activa de 5,2 kW con factor de potencia de 0,8 y corriente en atraso. Calcular la capacidad necesaria a conectar en paralelo para obtener un factor de potencia de 0,95.Solución
Calculamos primero ángulo de desfasaje inicial (Φ1) a partir del factor de potencia dado (Fp1). Sabemos que el factor de potencia es igual al coseno del ángulo y por lo tanto el ángulo lo calculamos con la función inversa del coseno.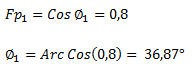
El triángulo de potencia nos queda con la siguiente forma:
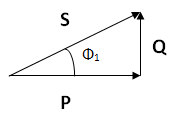
Calculamos por trigonometría el valor de la potencia reactiva inicial.
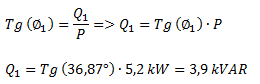
Buscamos un factor de potencia de 0,95, por lo tanto calculamos el ángulo deseado para ese nuevo factor de potencia.
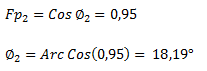
Calculamos la potencia reactiva total necesaria para obtener el ángulo hallado con la potencia activa dada.
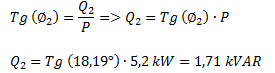
Calculamos la diferencia entre la potencia reactiva de la instalación y la potencia reactiva necesaria para obtener el factor de potencia solicitado.
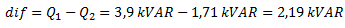
La diferencia entre ambas potencias es el valor de potencia reactiva que debe disminuirse. Debido a que la potencia reactiva de la instalación es del tipo inductiva (ya que se indica que la corriente está atrasada), para reducirla se debe generar una potencia reactiva capacitiva (que es de signo contrario).
Para calcular la capacidad utilizamos la siguiente expresión.
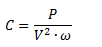
Calculamos la velocidad angular.
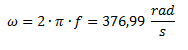
Calculamos la capacidad requerida para generar la diferencia de potencia calculada:
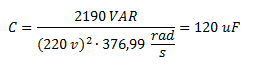
Ejercicio 2
Una instalación de 220 v y 60 Hz consume una potencia activa de 2500 W con un factor de potencia de 0,75 y corriente en atraso. Calcular la capacidad necesaria a conectar en paralelo para llevar el factor de potencia a 0,9.Solución
A partir del factor de potencia dado (Fp1) calculamos el ángulo de desfasaje inicial (Φ1) a través de la función inversa del coseno.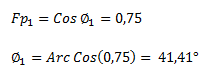
El triángulo de potencia nos queda con la siguiente forma:
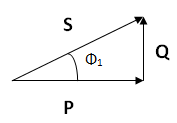
Calculamos el valor de la potencia reactiva inicial (cateto Q) utilizando la función tangente.
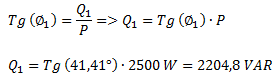
El factor de potencia buscado es de 0,9, por lo tanto calculamos el ángulo deseado para ese nuevo factor de potencia.
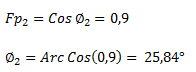
Calculamos la potencia reactiva necesaria para obtener el ángulo hallado.
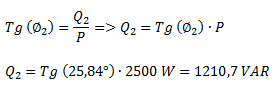
Calculamos la diferencia entre la potencia reactiva de la instalación y la potencia reactiva necesaria para obtener el factor de potencia solicitado.
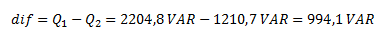
Sabemos que debemos disminuir la potencia reactiva en el valor de la diferencia hallada. Debido a que la instalación tiene una potencia reactiva inductiva (ya que la corriente está en atraso), buscamos un valor de capacidad que genere una potencia reactiva por esa diferencia. Como la potencia reactiva capacitiva es de signo contrario al de la potencia reactiva inductiva, podemos reducir ese valor.
Para calcular la capacidad utilizadnos la siguiente expresión:
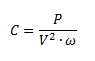
Calculamos la velocidad angular:
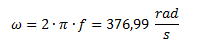
Calculamos la capacidad:
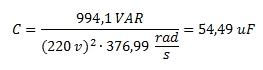
Seguir a calor
Volver a ejercicios de corriente alterna
Volver a home