Derivadas

La derivada de una función es la pendiente (o inclinación) de su recta tangente. Por lo tanto representa la rapidez con la que cambia la función en un determinado punto, es decir cuánto cambia el valor de su variable dependiente (“y”) ante cambios de su variable independiente (“x”).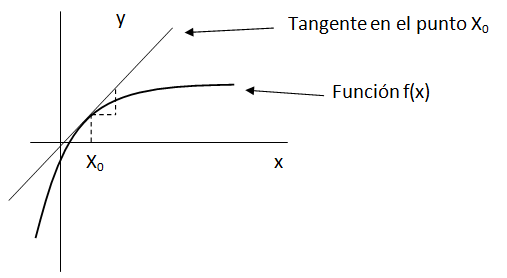



Podemos obtener la derivada de una función para un solo punto y en este caso será un valor numérico correspondiente a la pendiente de la recta tangente en ese punto o bien obtener una función derivada que es otra función que para cada valor de la variable “x” nos da como resultado el valor de la pendiente en ese punto. Esta función se llama función derivada.

Siempre debemos tener en cuenta que la función derivada no es la función tangente a la función original sino una función que al evaluarla en un determinado punto nos devuelve el valor de la pendiente de la recta tangente a la función original en ese punto.

Nomenclatura de derivadas

Más adelante detallaremos mejor la nomenclatura.

Ángulo de la recta tangente en un punto

Más arriba definimos a la derivada como la pendiente de la recta tangente, es decir que si tenemos el valor de una derivada en un punto podemos formar un triángulo rectángulo y por lo tanto conocer el valor del ángulo, tal como hacíamos con las rectas.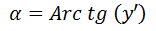

Cálculo de derivadas

Existen básicamente dos métodos de derivación, las derivadas por definición y las derivadas por regla. En las próximas secciones detallaremos ambos métodos.

Seguir a derivadas por definición
Volver a derivadas
Volver a home