Derivadas por definición

Si tenemos una función f(x) y queremos calcular su función derivada podemos utilizar la definición de derivada. Ésta nos dice que debemos hallar la pendiente de su recta tangente.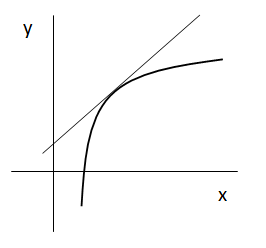



Para ello, elegimos un punto de la función al que llamamos x. Si evaluamos la función en “x” obtenemos un resultado f(x).



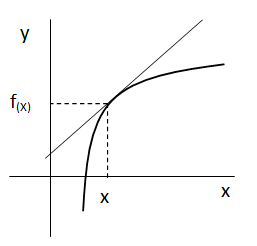
Sabemos que la pendiente de una recta es la variación en “y” sobre una variación en “x”. Entonces tomamos una distancia “h” a partir de “x” y volvemos a evaluar la función, en este caso en “x+h”.



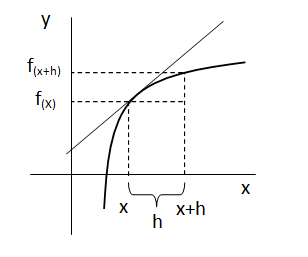
Ahora si consideramos un “h” tan pequeño como sea posible, podemos ver que tanto la función como la recta tangente se parecen, por lo tanto en ese caso podemos igualar los valores de la recta tangente a los valores que obtenemos de la función.



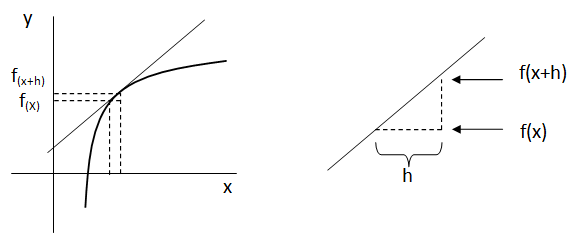
Finalmente la fórmula para calcular derivadas por definición la podemos plantear como un cociente entre las dos variaciones cuando la variación en “x” tiende a cero.

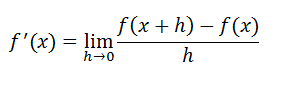
Ejemplo 1

Derivar por definición la función identidad f(x) = x.

Para resolver derivadas por definición escribimos la fórmula.



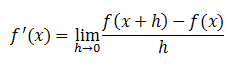
Luego evaluamos la función dada en “x+h” y en “x”. En este caso, como se trata de la función identidad, el resultado es el mismo:



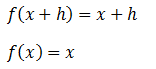
Reemplazamos los valores calculados en la fórmula y simplificamos:



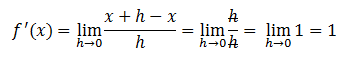
En este caso si bien calculamos la función derivada para todos los puntos (y no para uno solo), como podemos ver no aparece la variable “x” en la función derivada. Esto es porque la derivada vale “1” para todos los puntos. Tiene sentido ya que la pendiente de la función identidad es siempre “1” para todos los valores de “x”.

Ejemplo 2

Derivar por definición la función f(x) = x + 2.

Nuevamente escribimos la fórmula de derivada por definición.



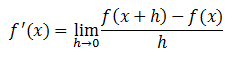
Ahora calculamos el valor de f(x+h), lo que significa evaluar la función en “x+h” o dicho de otra manera reemplazar el “x” de la función por el argumento en el cual la evaluamos que es “x+h”.



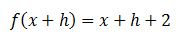
Luego evaluamos la función en “x”. No debemos reemplazar nada ya que se trata de la función original.



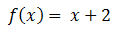
Por último reemplazamos en la fórmula los valores hallados y simplificamos.



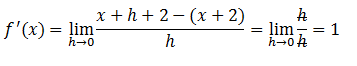
Nuevamente en este caso no aparece “x” en la función derivada ya que la pendiente de la función original es “1” para todos los valores de “x”.

Ejemplo 3

Derivar por definición la función f(x) = 2x – x².

Escribimos la fórmula de derivada por definición.



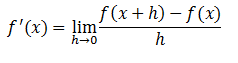
Calculamos f(x+h), lo que significa reemplazar cada “x” de la función original por “x+h”.



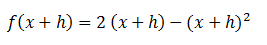
Aplicamos la propiedad distributiva y desarrollamos el cuadrado.



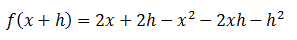
Reemplazamos los valores en la función original, simplificamos y calculamos el límite.



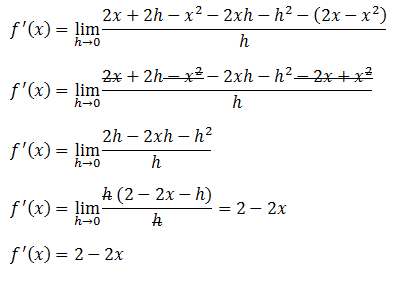
Seguir a derivadas por reglas
Volver a derivadas
Volver a home