Definición de vectores

Los vectores son objetos matemáticos que tienen un valor numérico, una dirección y un sentido. Gráficamente se representan como flechas que van desde un punto a otro. La longitud del vector corresponde a su valor numérico y se llama módulo. La inclinación determina su dirección. La flecha que se encuentra en uno de sus extremos determina el sentido.

Por ejemplo, el vector v = AB es aquel que se va desde el punto “A” al punto “B”.

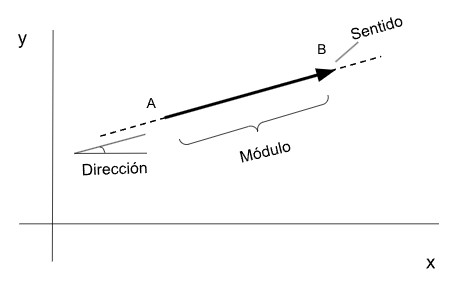
Equivalencia entre vectores

Dos vectores son equivalentes si tienen la misma longitud, dirección y sentido. En el siguiente gráfico podemos ver que el vector AB es equivalente al vector CD.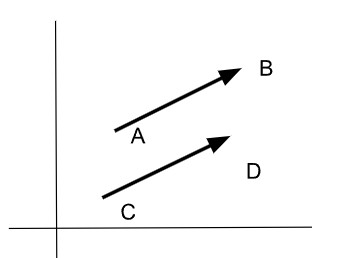



Los vectores usualmente se nombran con una letra minúscula. Cuando un vector va desde un punto “A” a un punto “B” se suele indicar como v = AB.

Sin embargo, usualmente trabajamos con vectores que tienen su origen en el origen de coordenadas, es decir en el punto (0, 0). De esta forma, al describir un vector solamente nombramos el punto al que llega mediante un par ordenado (x, y). Por ejemplo el vector (1,2) tiene origen de coordenadas (0, 0) y extremo en (1, 2).



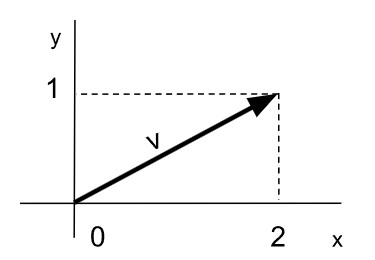
Generalmente los vectores se nombran con una letra minúscula. Por ejemplo:



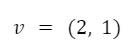
Para trasladar un vector desde un punto cualquiera hacia el origen de coordenadas simplemente restamos su extremo menos su origen.





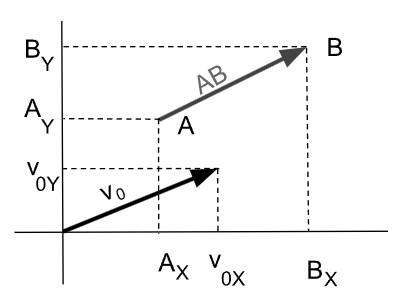
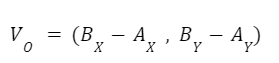
v₀ = Extremo del vector “v” trasladado al origen.
A_X, A_Y = Coordenadas del origen del vector a trasladar.
A_X, A_Y = Coordenadas del extremo del vector a trasladar.

También podemos trasladar un vector desde el origen a otro punto cualquiera. Para hacer esto sumamos su extremo al nuevo punto.



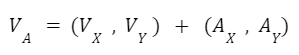
v_A = Extremo del vector “v” trasladado a “A”.
v_X, V_Y = Coordenadas del vector a trasladar.
A_X, A_Y = Coordenadas del punto hacia el cual se traslada.

Dimensiones de un vector

Cada vector está formado por componentes y la cantidad de componentes determina la dimensión del vector. Por ejemplo (1, 2) es un vector que tiene dos dimensiones, mientras que (1, 3, 4) es un vector que contiene tres.

Los vectores de dos dimensiones se utilizan para representar magnitudes en el plano mientras que los de tres dimensiones son utilizados para representar magnitudes en el espacio.



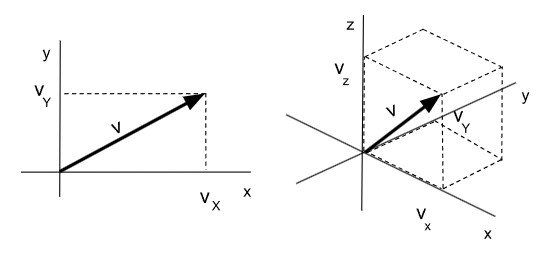
En diferentes ciencias y aplicaciones podemos encontrar vectores con más de tres dimensiones aunque los mismos no tengan una representación gráfica.

Vectores ortogonales

Dos vectores son ortogonales si forman un ángulo de 90 grados.

Vectores en física

En física utilizamos los vectores para representar magnitudes en las que además de un valor absoluto hay una dirección y un sentido. Por ejemplo fuerza, velocidad, aceleración, campo eléctrico, etc.


Seguir a representación de vectores
Volver a vectores
Volver a home