Definición de números complejos

Los números complejos son pares ordenados formados por una parte real y una parte imaginaria, que se escriben con la siguiente forma: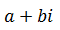



Son la suma de un número real (“a”) y un número imaginario (“bi”). Tanto “a” como “b” son números reales e “i” es la unidad imaginaria (por lo tanto “bi” es un número imaginario).

Los números complejos se aplican en diferentes ramas de la física, como por ejemplo en el estudio de circuitos de corriente alterna.

Para la unidad imaginaria normalmente se utiliza la letra “i” aunque en algunas aplicaciones puede usarse otra letra. Por ejemplo en el estudio de electricidad se suele utilizar la “j” para no confundirla con la intensidad. También la j puede aparecer antes del número que indica la cantidad imaginaria, de la siguiente manera:



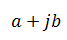
Dado que se trata de pares ordenados, los números complejos pueden ser representados en dos ejes cartesianos, al igual que los vectores de dos dimensiones. En el eje horizontal se ubica la parte real mientras que en el eje vertical se ubica la parte imaginaria.

Pueden ser expresados en forma binómica (con la forma a + bi) o en forma polar (indicando una longitud y un ángulo de inclinación sobre el eje horizontal). La conversión de una forma a la otra es similar a la conversión de vectores de dos dimensiones.


Seguir a representación de números complejos
Volver a números complejos
Volver a home