
Clasificación de ecuaciones diferenciales
Por su naturaleza
Ecuaciones diferenciales ordinarias: Son ecuaciones diferenciales que involucran la derivada de una sola variable independiente. Se conocen por sus siglas como EDO. Los siguientes son algunos ejemplos de EDO: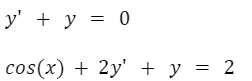
Ecuaciones diferenciales parciales: Son ecuaciones diferenciales que involucran derivadas parciales de varias variables. Se conocen por sus siglas como EDP. Los siguientes son algunos ejemplos de EDP:
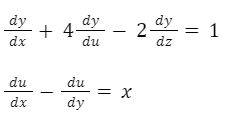
Por su orden
El orden de una ecuación diferencial corresponde al orden más alto de las derivadas que aparecen. La siguiente es una ecuación diferencial de primer orden: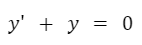
La siguiente, en cambio, es una ecuación diferencial de segundo orden:
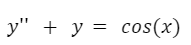
Por su linealidad
Ecuaciones diferenciales lineales: Una ecuación diferencial es lineal si la función desconocida (normalmente representada por la letra “y”) y sus derivadas aparecen en forma lineal. Esto significa que no tienen exponentes distintos de cero o uno, ni aparecen dentro de operaciones trigonométricas, logarítmicas, etc.En general, estas ecuaciones tienen o se pueden llevar a la siguiente forma:
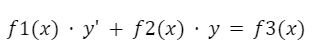
En la expresión anterior, f1, f2 y f3 son funciones que dependen únicamente de la variable “x”. Los siguientes son ejemplos de ecuaciones diferenciales lineales:
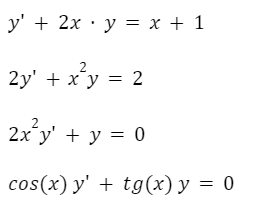
Como vemos, pueden aparecer exponentes, logaritmos, etc. en la ecuación, pero siempre y cuando no aparezcan en la variable dependiente o en sus derivadas.
Recordemos que una función de “x” podría ser igual a “1” por lo tanto no es necesario la presencia de una función de “x” en la expresión. Por ejemplo, la siguiente ecuación diferencial también es lineal:
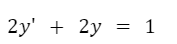
Ecuaciones diferenciales no lineales: Las funciones y sus derivadas no son lineales. Aparecen exponentes, logaritmos, funciones trigonométricas, etc. en las variables dependientes o en sus derivadas. Los siguientes son ejemplos de ecuaciones diferenciales no lineales:
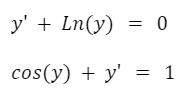
Seguir a clasificación de las soluciones
Volver a ecuaciones diferenciales
Volver a home