
Conversión de vectores
De forma binómica a forma polar
Cuando tenemos un vector en forma binómica lo que tenemos es el valor de sus dos componentes (AX y AY) y al pasarlo a forma polar buscamos la longitud de la flecha (o módulo) y el ángulo sobre el eje horizontal.Como se trata de un triángulo lo podemos resolver aplicando el teorema de Pitágoras y las relaciones trigonométricas.
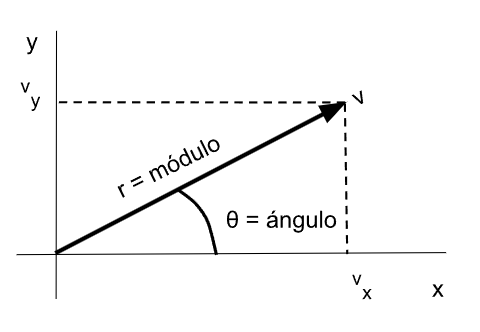
El módulo del vector se puede obtener con el teorema de Pitágoras, como la raíz cuadrada de la suma del cuadrado de sus componentes.
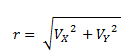
Para obtener el ángulo utilizamos una relación trigonométrica. Lo que buscamos es el ángulo desde el eje horizontal y tomado en sentido antihorario comenzando en el primer cuadrante. Por ejemplo, si el vector está en el primer cuadrante podemos utilizar la siguiente expresión:
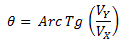
Si el vector está en otro cuadrante podemos calcular un ángulo también mediante la inversa de la tangente y luego sumar o restar ángulos de tal forma de obtener el ángulo medido desde el origen de coordenadas polares.
De forma polar a forma binómica
La conversión de forma polar a binómica consiste en hallar las longitudes de las proyecciones del vector sobre cada eje. Debido a que el módulo del vector es la hipotenusa de un triángulo, podemos hallar los dos catetos restantes mediante relaciones trigonométricas.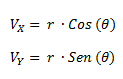
Seguir a módulo de un vector
Volver a vectores
Volver a home