Clasificación de las soluciones de una ecuación diferencial
Encontrar la solución de una ecuación diferencial consiste en hallar una función tal que se cumpla la igualdad planteada en la ecuación. Esta solución puede clasificarse de la siguiente manera:Solución general
Sabemos que diferentes funciones pueden tener una misma derivada debido a que la derivada de una constante es igual a cero. Entonces, si derivamos dos funciones que difieran en su término constante obtendremos la misma derivada. Por ejemplo, veamos las siguientes funciones: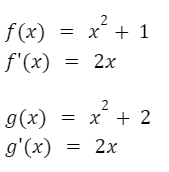
Debido a lo anterior, cuando integramos una función su respuesta incluye una constante de integración que contempla a una familia de funciones. En las ecuaciones diferenciales ocurre lo mismo. Si no hay condiciones iniciales podemos tener infinitas funciones que cumplan la igualdad expresada en la ecuación diferencial. A este conjunto de soluciones se lo denomina solución general. Por ejemplo, veamos la siguiente ecuación diferencial:
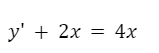
Su solución es cualquier función con la forma:
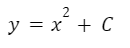
A la expresión anterior se la denomina solución general.
Solución particular
Un determinado problema puede tener ciertas condiciones como por ejemplo un valor por el que deba pasar la función solución. Esto hace que exista una única función (del conjunto de funciones que son solución) que cumpla esa condición y se la llama solución particular.Supongamos que la siguiente función es solución a una ecuación diferencial:
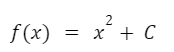
Pero además existe una condición que indica:
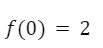
Entonces habrá una única función solución:
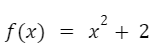
Este tema se explica con más detalle en la sección de ecuaciones diferenciales con valor inicial.
Volver a ecuaciones diferenciales
Volver a home