Representación fasorial
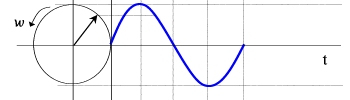
La corriente alterna se puede representar con una flecha girando a velocidad angular ω. Este elemento recibe el nombre de fasor y se representa como un número complejo.Su longitud coincide con el valor máximo de la tensión o corriente (según sea la magnitud que se esté representando). También se utiliza el valor RMS en lugar del valor máximo (ver transformación a fasores). En ese caso habría que dividir el valor máximo por raíz de 2.
El ángulo (corrimiento de la señal sobre el eje horizontal) representa la fase. La velocidad de giro ω está relacionada con la frecuencia de la señal.
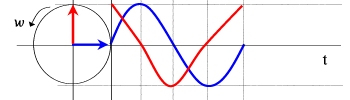
En muchas ocasiones, las tensiones y las corrientes de circuitos con corriente alterna presentan desfasajes entre sí (corrimientos horizontales). En los diagramas fasoriales esto se representa con un ángulo entre los fasores. En el ejemplo siguiente hay dos señales desfasadas 90° y a la izquierda de las mismas se pueden ver los dos fasores con un ángulo de 90 grados entre sí.
En un diagrama fasorial quedarían representadas de la siguiente manera:
Al igual que los números complejos, los fasores pueden estar representados en forma binómica o polar (también existen otras como la trigonométrica y la exponencial). En algunos casos nos conviene una forma de expresarlos y en otros casos será más simple hacer cuentas con la otra forma.
Forma polar
Los fasores pueden describirse matemáticamente en forma polar, es decir como un módulo y un ángulo. A continuación vamos a ver un ejemplo de cómo indicar una tensión alterna con un fasor.Supongamos que tenemos la siguiente expresión de tensión:
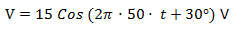
La expresión anterior se puede representar como un fasor indicando la tensión máxima (15 V en el ejemplo) y el ángulo de desplazamiento (30° en el ejemplo). En forma polar, la tensión anterior queda representada por el siguiente fasor:
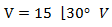
Gráficamente lo podemos ver de la siguiente forma:
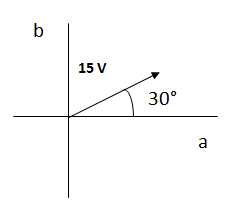
Como convención, las señales deben estar expresadas con una función coseno y con un valor positivo para realizar un análisis fasorial. En caso de no estar expresadas de esta manera debemos convertirlas. Esto se explica detalladamente en la próxima sección.
Forma binómica
Otra forma de expresar a un fasor, es la forma binómica, es decir como: a + j b siendo a la parte real y b la parte imaginaria.La señal del ejemplo anterior la podemos expresar en base a sus componentes rectangulares como:
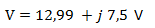
Gráficamente nos queda el diagrama de la siguiente manera:
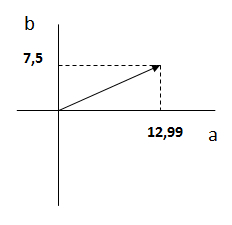
Conversión de fasores
Es posible convertir fácilmente un fasor de la forma polar a la forma binómica y viceversa. Para ello se utilizan los mismos conceptos que para convertir números complejos entre ambas formas de representación.Puede consultarse más sobre la conversión en la sección de números complejos.
Seguir a transformación a fasores
Volver a corriente alterna
Volver a home