Resolución de circuitos en corriente continua
Al resolver un circuito buscamos hallar sus distintas variables tales como la corriente, la caída de tensión y la potencia disipada en cada uno de sus componentes.Una forma de hacer esto es ir agrupando los componentes en componentes equivalentes para hallar las corrientes y tensiones totales. Luego, aplicando las leyes ya estudiadas, podemos ir analizando lo que sucede en cada componente.
Ejemplo de cálculo de circuito resistivo
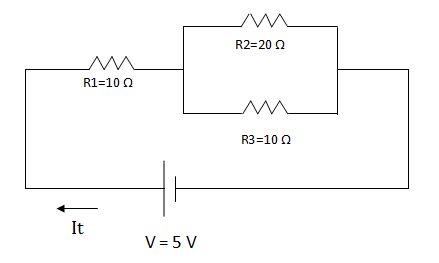
En primer lugar calculamos la asociación en paralelo de las resistencias 2 y 3.
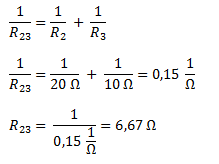
Obtenemos un circuito equivalente
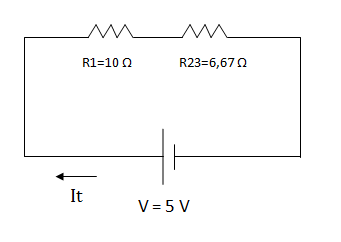
Luego calculamos la asociación de resistencias de R1 con R23 que se encuentran en serie y que llamamos R123.
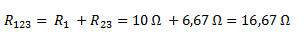
Obtenemos un nuevo circuito equivalente con R123 que también es la resistencia total.
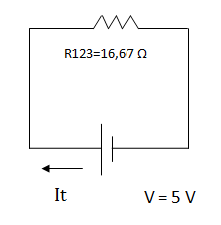
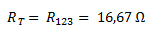
Calculamos la intensidad total por medio de la ley de Ohm
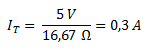
Sabemos que I1 es igual a la intensidad total ya que pertenece a la misma rama.
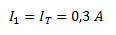
Con el valor de resistencia y corriente en R1 podemos calcular su caída de tensión.
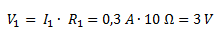
La caída de tensión en las resistencias en paralelo (V23) es igual a la tensión en cada una de las dos resistencias y es igual a la tensión total menos la caída en R1.
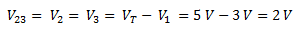
Con las caídas de tensión en R2 y en R3 podemos calcular la corriente por cada una de esas dos resistencias aplicando la ley de Ohm.
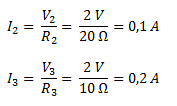
Por último calculamos la potencia disipada en cada resistencia multiplicando su caída de tensión por la corriente que circula por la misma.
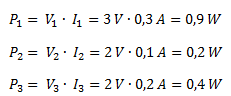
La potencia total la podemos calcular como el producto de la tensión total aplicada por la corriente total del circuito.
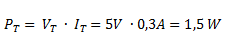
También podríamos calcularla como la suma de las potencias que disipa cada resistencia.
Volver a corriente continua y circuitos
Volver a home