Producto vectorial
El producto vectorial es una multiplicación entre vectores que da como resultado otro vector ortogonal a ambos.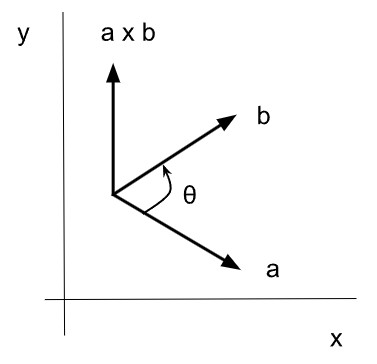
Cálculo del producto vectorial a partir de coordenadas cartesianas
Dados dos vectores “a” y “b” como los siguientes: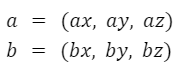
El producto vectorial se expresa como un vector de tres componentes.
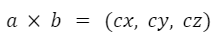
Las componentes se calculan de la siguiente forma:
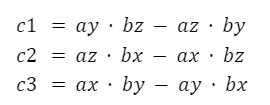
La fórmula anterior se obtiene a partir de un determinante. Planteándose de esa manera es más fácil de recordar.
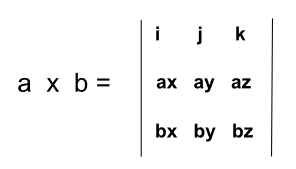
Cálculo del producto vectorial a partir de coordenadas polares
El módulo se calcula como el producto de los módulos de los vectores multiplicado por el seno del ángulo que los separa.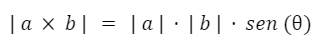
La dirección es sobre la recta ortogonal a ambos vectores, es decir que forma 90 grados con los mismos.
El sentido se calcula con la regla de la mano derecha, en donde el pulgar indica el sentido del vector resultado. Esto quiere decir que en el producto vectorial importa el orden en que se multiplican los vectores, ya que determina el sentido del vector resultado.
Propiedades del producto vectorial
El producto vectorial no es conmutativo. Sin embargo, el resultado es un vector igual pero de signo contrario.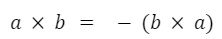
El producto vectorial es distributivo con respecto a la suma de vectores.
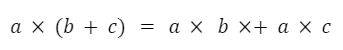
Si el producto vectorial entre dos vectores es igual a cero y ninguno de los vectores es cero entonces ambos vectores son paralelos.
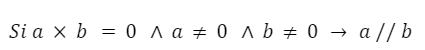
El producto vectorial de un vector consigo mismo es igual al vector nulo.
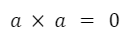
El producto de un vector por un escalar es asociativo con el producto vectorial.
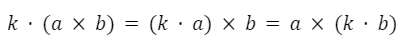
Seguir a ejercicios resueltos de vectores
Volver a vectores
Volver a home