Gradiente

El gradiente es un vector que representa la dirección y la magnitud de la máxima tasa de crecimiento de una función escalar en un punto dado, es decir, es un concepto similar al de derivada pero generalizado a funciones n-dimensionales.

Dada una función escalar, el gradiente es un campo vectorial debido a que se representa con un vector en cada punto de un espacio n-dimensional y que apunta hacia donde más crece la función en ese lugar.

El concepto de gradiente tiene importantes aplicaciones en la física, la ingeniería y otras áreas de conocimiento. Dada una función “f”, el gradiente se representa como ∇f o grad(f).

Cálculo del gradiente

El gradiente se obtiene expresando un vector cuyas componentes son las derivadas parciales de la función para cada una de sus variables independientes.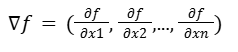

Propiedades del gradiente

El gradiente de una suma de funciones es igual a la suma de los gradientes de cada función.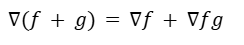



El gradiente del producto entre un escalar y una función es igual al producto del escalar por el gradiente.



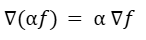
El gradiente es ortogonal a las superficies de nivel de la función.

Ejemplo de cálculo del gradiente

Dada la función “f”: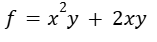



Su gradiente se calcula como un vector cuyas componentes son las derivadas parciales de “f” respecto a cada una de las variables independientes.





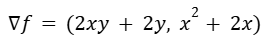
Seguir a aplicaciones de las derivadas
Volver a derivadas
Volver a home