Ejercicios de transformación a coordenadas polares
Obtener las coordenadas polares de los siguientes vectores:- V1 = (1, 2)
- V2 = (-3, 1)
- V3 = (-2, -2)
- V4 = (2, -1)
Solución
Para el vector V1Graficamos el vector en base a sus coordenadas cartesianas:
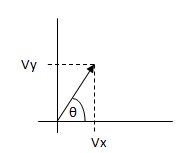
El módulo del vector lo calculamos siempre como la raíz cuadrada de sus componentes al cuadrado.
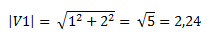
El ángulo lo calculamos por trigonometría.
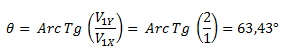
Expresamos el resultado en forma polar (módulo y ángulo).
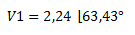
Para el vector V2
Graficamos el vector en base a sus coordenadas cartesianas:
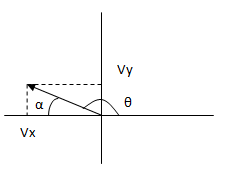
Calculamos el módulo:
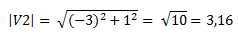
Con la inversa de la tangente obtenemos un ángulo α, desde el eje horizontal pero que no está tomado desde el primer cuadrante.
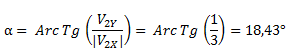
Para obtener el ángulo desde el primer cuadrante restamos el ángulo obtenido a 180°.
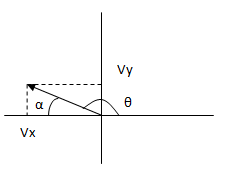
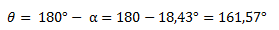
Finalmente el resultado nos queda de la siguiente manera:
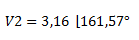
Para el vector V3
Graficamos el vector en base a sus componentes cartesianas:
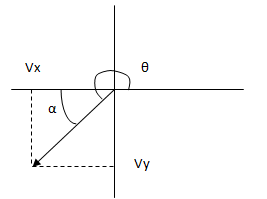
Calculamos su longitud:
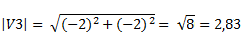
Con la inversa de la tangente obtenemos un ángulo α, desde el eje horizontal pero que no está tomado desde el primer cuadrante.
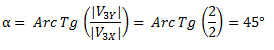
Para obtener el ángulo buscado le sumamos 180° al ángulo obtenido.
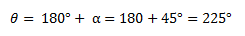
Finalmente nos queda el vector en coordenadas polares de la siguiente manera:
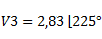
Para el vector V4
Graficamos el vector en base a sus coordenadas cartesianas:
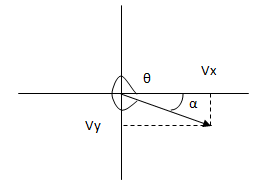
Calculamos su longitud:
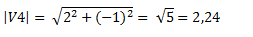
Con la inversa de la tangente obtenemos un ángulo α, desde el eje horizontal pero que no está tomado desde el primer cuadrante.
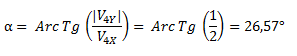
Para obtener el ángulo buscado le restamos el ángulo obtenido a 360°.
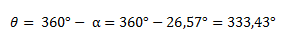
Finalmente nos queda el vector expresado de la siguiente manera:
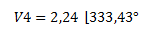
Seguir a ejercicios de transformación a coordenadas cartesianas
Volver a ejercicios de vectores
Volver a home