
Ejercicios de suma analítica de fuerzas
Ejercicio 1
Sumar analíticamente las siguientes fuerzas.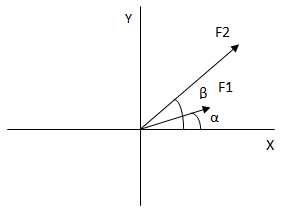
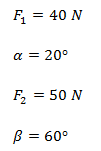
Solución
Hallamos las componentes cartesianas de las fuerzas.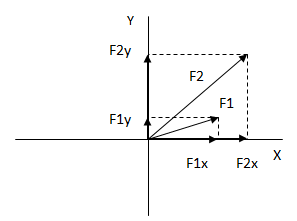
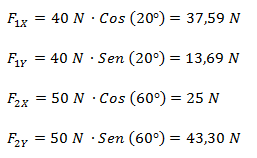
Planteamos la sumatoria de fuerzas por cada eje.
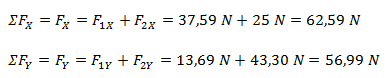
Luego de hacer la sumatoria de fuerzas nos queda una fuerza resultante por cada eje (dos vectores con una componente distinta de cero y otra componente igual a cero), lo que equivale a un solo vector expresado en forma binómica.
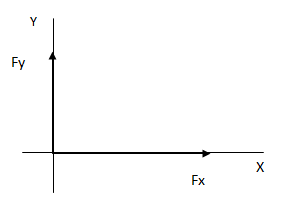
Para hallar el resultado componemos ambas fuerzas en una sola, lo que equivale a convertir el vector a forma polar.
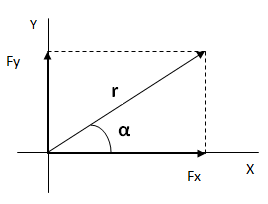
El módulo lo calculamos por el teorema de Pitágoras ya que corresponde a la hipotenusa de un triángulo rectángulo.
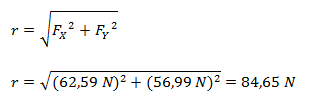
El ángulo lo calculamos por trigonometría a través de la función tangente.
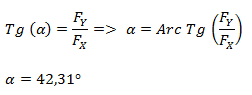
Ejercicio 2
Sumar analíticamente las siguientes fuerzas.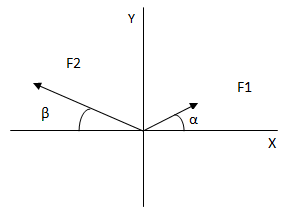
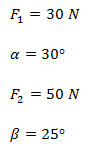
Solución
Hallamos las componentes cartesianas de las fuerzas.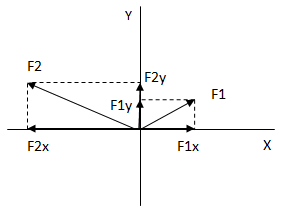
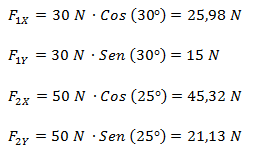
Debemos cambiar el signo de F2X ya que, como puede verse en el gráfico, la misma tiene signo negativo. El resultado dio positivo ya que no tomamos el ángulo desde el eje x en el primer cuadrante.
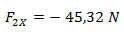
En caso de que hubiéramos tomado el ángulo desde el primer cuadrante (180° – 25° = 155°) ya nos habría dado con signo negativo.
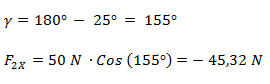
Planteamos la sumatoria de fuerzas por cada eje:
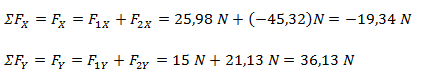
Luego de hacer la sumatoria de fuerzas nos queda una fuerza resultante por cada eje (dos vectores con una componente distinta de cero y otra componente igual a cero), lo que equivale a un solo vector expresado en forma binómica.
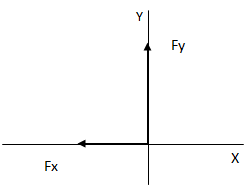
Para hallar el resultado componemos ambas fuerzas en una sola, lo que equivale a convertir el vector a forma polar.
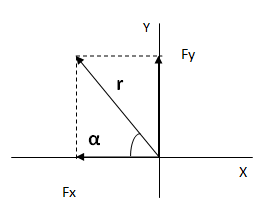
El módulo lo calculamos por el teorema de Pitágoras.
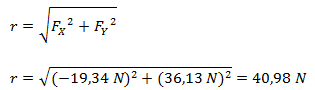
El ángulo lo calculamos por trigonometría a través de la función tangente.
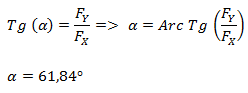
El ángulo obtenido corresponde al ángulo desde el eje X pero tomado en el segundo cuadrante. Sin embargo, para expresar correctamente el vector, necesitamos tener el ángulo desde el origen de coordenadas polares, es decir desde el primer cuadrante. Para ello, restamos el ángulo obtenido a 180°.
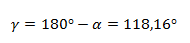
Ejercicio 3
Sumar analíticamente las siguientes fuerzas.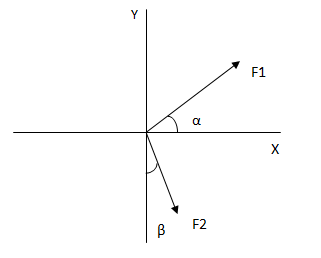
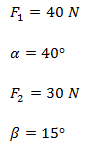
Solución
Hallamos las componentes cartesianas de las fuerzas.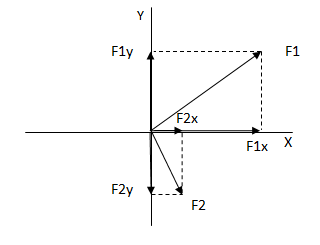
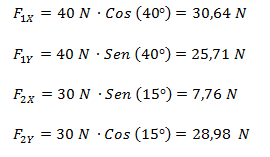
Debemos cambiar el signo de F2Y ya que, como puede verse en el gráfico, la misma tiene sentido contrario al sistema de coordenadas. El resultado dio positivo ya que no tomamos el ángulo desde el eje x en el primer cuadrante.
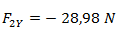
En caso de que hubiéramos tomado el ángulo desde el primer cuadrante (270° + 15° = 285°) y además hubiéramos utilizado la función seno ya nos habría dado con signo negativo. Recordemos que con la función seno podemos obtener las componentes verticales pero tomando los ángulos desde el origen.
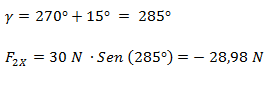
Planteamos la sumatoria de fuerzas por cada eje.
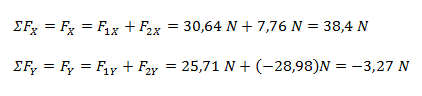
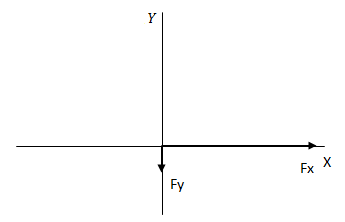
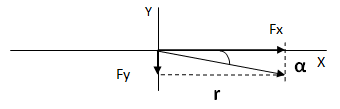
Para hallar el resultado componemos ambas fuerzas en una sola, lo que equivale a convertir el vector a forma polar.
El módulo lo calculamos por el teorema de Pitágoras.
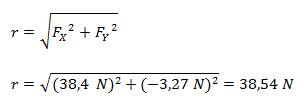
El ángulo lo calculamos por trigonometría a través de la función tangente.
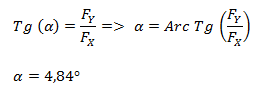
El ángulo obtenido corresponde al ángulo desde el eje X pero tomado en el cuarto cuadrante. Sin embargo, para expresar correctamente el vector, necesitamos tener el ángulo desde el origen de coordenadas polares, es decir desde el primer cuadrante. Para ello, restamos el ángulo obtenido a 360°.
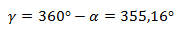
Ejercicio 4
Sumar analíticamente las siguientes fuerzas.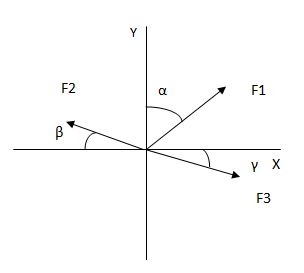
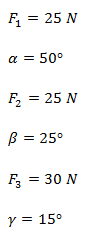
Solución
Hallamos las componentes cartesianas de las fuerzas.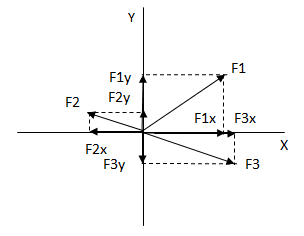

Debemos cambiar el signo de F2X y de F3Y ya que, como puede verse en el gráfico, las mismas tienen sentido contrario al sistema de coordenadas. El resultado dio positivo ya que no tomamos el ángulo desde el eje x en el primer cuadrante.
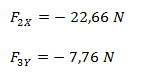
En caso de que hubiéramos tomado los ángulos desde el primer cuadrante (155° y 345° respectivamente) y además hubiéramos utilizado la función seno para las componentes verticales y coseno para las componentes horizontales ya nos habría dado con signo negativo.
Planteamos la sumatoria de fuerzas por cada eje.
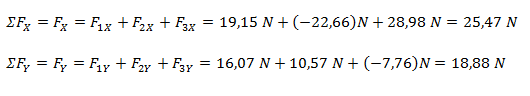
Luego de hacer la sumatoria de fuerzas nos queda una fuerza resultante por cada eje (dos vectores con una componente distinta de cero y otra componente igual a cero), lo que equivale a un solo vector expresado en forma binómica.
Para hallar el resultado componemos ambas fuerzas en una sola, lo que equivale a convertir el vector a forma polar.
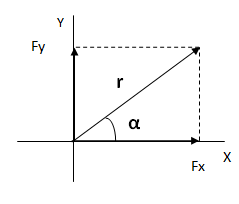
El módulo lo calculamos por el teorema de Pitágoras.
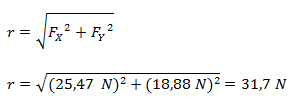
El ángulo lo calculamos por trigonometría a través de la función tangente.
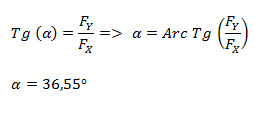
Seguir a ejercicios de fuerza gravitatoria
Volver a ejercicios de fuerzas
Volver a home