
Ejercicios resueltos de oscilaciones amortiguadas
Ejercicio 1
En un oscilador amortiguado, la fuerza de amortiguamiento es de 1 N cuando la velocidad es de 5 m/s. Calcular la constante de amortiguamiento debido a la viscosidad.Solución
La constante de amortiguamiento debido a la viscosidad se define como la fuerza de amortiguamiento por unidad de velocidad. Planteamos ese cociente y realizamos la división.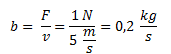
Ejercicio 2
Un oscilador amortiguado está formado por una masa de 40 g y un resorte de constante elástica k=20 N/m. La constante de amortiguamiento debido a la viscosidad es de 0,05 kg/s y la amplitud del movimiento es de 0,3 m. En el instante inicial el cuerpo se encuentra en la posición 0,3 m.Calcular la velocidad angular, la frecuencia, el factor de calidad y la posición para t = 0,15 s.
Solución
Calculamos la velocidad angular utilizando la fórmula de velocidad angular para oscilaciones amortiguadas.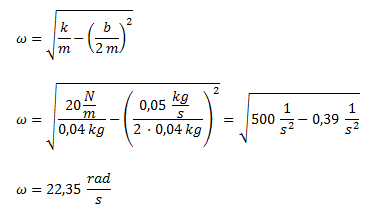
Despejamos la frecuencia de la fórmula de la definición de velocidad angular.
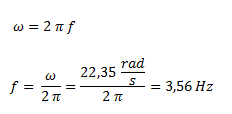
Calculamos el factor de calidad.
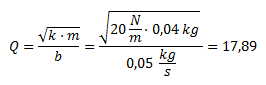
Calculamos la fase. Como en el instante inicial el cuerpo se encuentra en la posición de desplazamiento máximo positivo, la fase es 0 radianes.
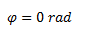
Planteamos la ecuación horaria para un oscilador amortiguado, reemplazamos por los valores obtenidos y calculamos el resultado.
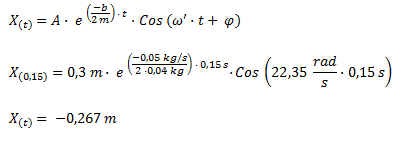
Ejercicio 3
Una masa de 250 g se encuentra unida a un resorte de constante elástica k = 50 N/m y oscila de manera amortiguada. La constante de amortiguamiento debido a la viscosidad es de 0,1 kg/s.Calcular:
- El período de las oscilaciones.
- El tiempo para que la amplitud decrezca a la mitad.
- El tiempo para que la energía mecánica sea del 40 % de la energía original.
Solución
Calculamos la velocidad angular para oscilaciones amortiguadas.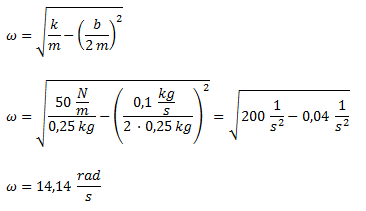
Despejamos la frecuencia de la fórmula de velocidad angular y reemplazamos el valor calculado.
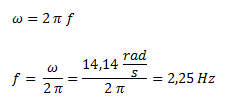
Calculamos el período como la inversa de la frecuencia.
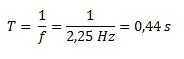
Para calcular el tiempo en el que la amplitud decrece a la mitad planteamos la fórmula de amplitud en función del tiempo (sabiendo que la amplitud final debe ser la mitad de la amplitud inicial) y despejamos el tiempo.
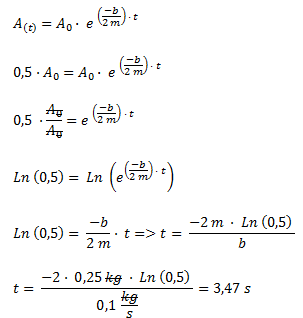
Hacemos lo mismo para la energía mecánica, sabiendo que la energía mecánica final debe ser un 40% de la energía mecánica original.
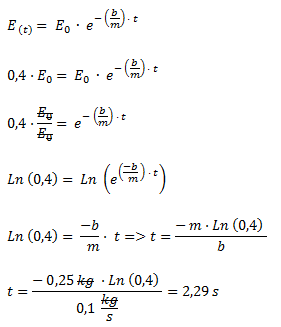
Ejercicio 4
Un oscilador amortiguado está formado por una masa de 150 g. La amplitud inicial es de 0,25 m. En 10 segundos la amplitud disminuye a 0,15 m.Calcular la constante de amortiguamiento debido a la viscosidad.
Solución
Planteamos la fórmula de amplitud respecto del tiempo, reemplazamos por los valores conocidos y despejamos b.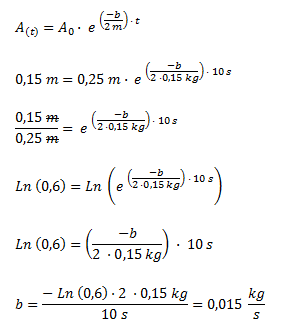
Seguir a hidráulica
Volver a oscilaciones amortiguadas
Volver a home