
Ejercicios de movimiento circular uniformemente variado
Ejercicio 1
Una turbina de un metro de diámetro se pone en marcha en t=0 y a los 20 segundos alcanza una velocidad de 3000 RPM. Calcular la aceleración angular y la aceleración tangencial.Solución
En primer lugar convertimos las revoluciones por minuto a revoluciones por segundo, es decir a hertz.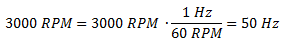
Luego calculamos la velocidad angular final.
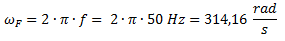
Calculamos la aceleración angular en base a su definición, es decir como la variación de la velocidad angular sobre la variación de tiempo.
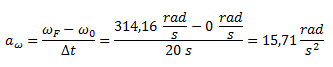
Como ya tenemos calculada la aceleración angular, podemos calcular la aceleración tangencial directamente:
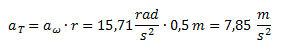
Ejercicio 2
Un móvil que se encuentra en MCU recorre una circunferencia de 100 metros de diámetro cada 30 segundos. En t=0 comienza a disminuir su velocidad hasta que se detiene completamente a los 15 segundos. Calcular la aceleración angular y tangencial.Solución
Calculamos la velocidad angular inicial en base a su definición (variación de ángulo sobre variación de tiempo). Sabemos que recorre una circunferencia completa (2π radianes) en 30 segundos.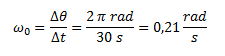
La velocidad angular final es cero ya que el móvil se detiene.
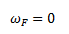
Calculamos la aceleración angular en base a su definición.
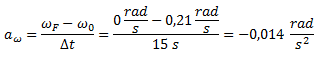
Como ya tenemos calculada la aceleración angular, podemos calcular directamente la aceleración tangencial multiplicándola por el radio y sin necesidad de plantear la definición (variación de velocidad sobre variación de tiempo).
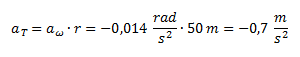
Seguir a estática y dinámica
Volver a MCUV
Volver a home