
Ejercicios de movimiento circular uniforme
Ejercicio 1
Un móvil se desplaza con una trayectoria circular a una velocidad de 2 m/s.¿Cuánto tardará en dar dos vueltas alrededor de una circunferencia de 100 metros de diámetro?
Solución
Podemos plantear el problema con las ecuaciones de velocidad tangencial (sabiendo que tiene que recorrer dos veces el perímetro) o de velocidad angular (sabiendo que tiene que recorrer dos veces el ángulo de la circunferencia completa, es decir 2π).Dado que tenemos la velocidad tangencial vamos a plantear su ecuación y despejar el tiempo. Recordemos que la velocidad tangencial es la variación de posición respecto del tiempo.
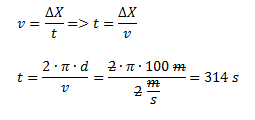
Ejercicio 2
Un móvil da tres vueltas sobre una circunferencia de 300 metros de diámetro a velocidad constante y tarda 2 minutos en hacerlo.Calcular:
- Frecuencia
- Período
- Velocidad angular
- Velocidad tangencial
- Aceleración centrípeta
Solución
Convertimos las el tiempo a segundos.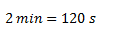
Calculamos la frecuencia a través de su definición.
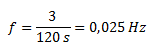
Calculamos el período como la inversa de la frecuencia.
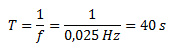
Obtenemos la velocidad angular a partir de la frecuencia.
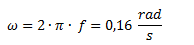
También podríamos haber obtenido esta velocidad en base a su definición, es decir la variación de ángulo sobre la variación de tiempo sabiendo que recorre 3 vueltas (6 π radianes) en 120 segundos.
Calculamos la velocidad tangencial multiplicando la velocidad angular (en radianes) por el radio.
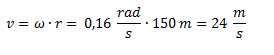
Otra manera de haberla calculado es a través de su definición, es decir haciendo el cociente entre el espacio recorrido y el tiempo empleado, sabiendo que recorrió el perímetro de la circunferencia tres veces en 120 segundos.
Por último hallamos la aceleración centrípeta.
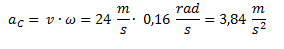
Ejercicio 3
Un móvil se desplaza a velocidad constante de 2,25 m/s sobre una circunferencia de 50 metros de diámetro.¿Qué distancia y que ángulo habrá recorrido a los 10 segundos de comenzado el movimiento?
Solución
Planteamos la ecuación horaria de la posición respecto del tiempo y reemplazamos por los valores del ejercicio.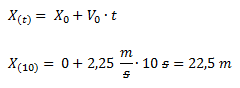
Para calcular el ángulo recorrido podemos plantear la ecuación horaria de posición angular o bien, ya que tenemos calculada la distancia recorrida en ese tiempo, podemos dividirla por el radio ya que ambas magnitudes están relacionadas por la siguiente expresión.
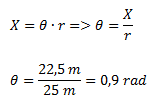
Seguir a MCUV
Volver a MCU
Volver a home