Ejercicios resueltos de movimiento armónico simple

Ejercicio 1

Un objeto describe un movimiento armónico simple cuya amplitud es de 0,5 m y su frecuencia de oscilación es de 2 Hz. En el instante inicial se encuentra en X = 0,5 m.

Escribir las ecuaciones de posición, velocidad y aceleración en función del tiempo.

Calcular la posición, la velocidad y la aceleración para t = 0,35 s.

Solución

Calculamos la velocidad angular mediante su fórmula, es decir como el producto del 2π por la frecuencia.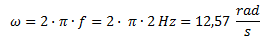



Determinamos el ángulo de fase. Dado que en el instante t = 0 el móvil se encuentra en el desplazamiento máximo positivo, podemos ver que no hay desplazamiento con respecto a una función coseno, es decir que la fase es de 0 radianes.



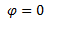
Planteamos las ecuaciones de posición, velocidad y aceleración. No hace falta indicar la fase dentro del argumento de la función ya que la misma es 0.



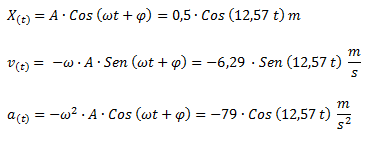
Calculamos la posición, la velocidad y la aceleración para t = 0,35 s.

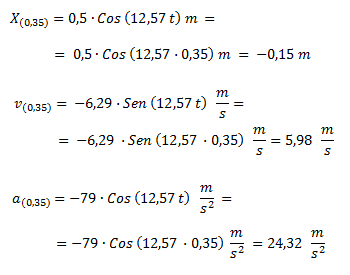
Ejercicio 2

Un oscilador armónico describe un movimiento según la siguiente función.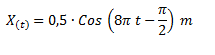



Indicar la velocidad angular, la frecuencia de oscilación, la velocidad máxima y la aceleración máxima.

Solución

La velocidad angular la obtenemos directamente de la expresión dada.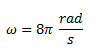



Despejamos la frecuencia de la fórmula de velocidad angular y reemplazamos los valores.



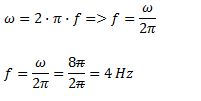
La velocidad máxima y la aceleración máxima se calculan con sus respectivas fórmulas. Recordemos que estas formulas son similares a las de velocidad y aceleración en función del tiempo, reemplazando por “1” a la función coseno (ya que ese el máximo valor que esa función puede alcanzar) y expresando el resultado en forma positiva.

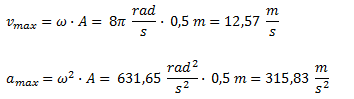
Ejercicio 3

Un oscilador armónico describe un movimiento según la siguiente expresión: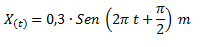



Expresar la posición mediante una función coseno positiva y escribir las ecuaciones de velocidad y aceleración en función del tiempo.

Solución

Para convertir una función seno positiva en una función coseno positiva debemos restarle a la fase 90° (es decir π/2), ya que la función coseno se encuentra adelantada 90° con respecto a la función seno. Debido a que la fase dada es π/2, la fase para la función coseno es 0.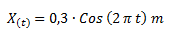



De la ecuación calculada, obtenemos la amplitud, la velocidad angular y la fase.



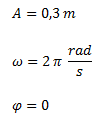
En base a los datos anteriores indicamos las ecuaciones de velocidad y aceleración en función del tiempo.




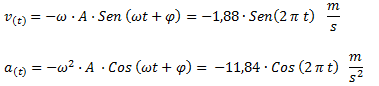
Seguir a oscilaciones amortiguadas
Volver a movimiento armónico simple
Volver a home