Ejercicios de leyes de Kirchhoff

Ejercicio 1

Calcular la corriente por la rama 3, sabiendo que I₁ = 4 A e I₂ = 3 A.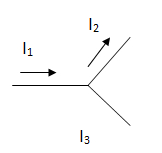

Solución

Planteamos la ley de Nodos.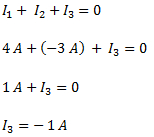



La corriente es saliente del nodo.

Ejercicio 2

Calcular la corriente por la rama 3, sabiendo que I₁ = 2 A e I₂ = 4 A.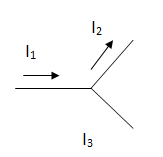

Solución

Planteamos la ley de Nodos.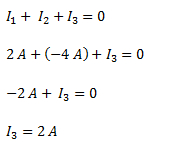



La corriente es entrante al nodo.

Ejercicio 3

Hallar la corriente I₃.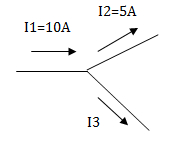

Solución

Planteamos un sistema de referencia relativo al nodo y tomamos las corrientes entrantes como positivas y las salientes como negativas.

I₁ = entrante, entonces es positiva
I₂ = saliente, entonces es negativa

Si bien I₂ es positiva en base a su flecha (su propio sistema de referencia) es negativa con respecto al nodo ya que es una corriente saliente.

Sabemos que la suma algebraica de corrientes en el nodo es igual a 0, entonces escribimos la ecuación.



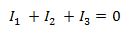
Reemplazamos los valores conocidos:



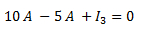
Despejamos I₃:



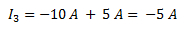
Con respecto al nodo la corriente I₃ es de 5 A y es negativa ya que es saliente. Sin embargo, para el sistema de referencia de I₃ (su flecha), la corriente es positiva 5 [A].

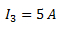
Ejercicio 4

Hallar la corriente I₃.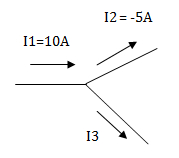

Solución

Identificamos el sentido de las corrientes con respecto al nodo. En el caso de I₂ la corriente tiene un signo negativo, por lo que el sentido es contrario al de su flecha, es decir entrante al nodo y por lo tanto, con respecto al nodo tiene signo positivo.

I₁ = entrante, entonces es positiva
I₂ = entrante, entonces es positiva

Planteamos la ley de nodos y reemplazamos por los valores del ejercicio:



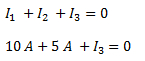
Despejamos la corriente I₃:



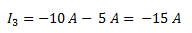
La corriente es de -15 [A] con respecto al nodo y de 15[A] con respecto a la flecha de I₃.

Ejercicio 5

Obtener la tensión aplicada a la rama AB a partir de las caídas de tensión indicadas.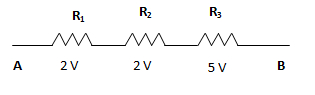

Solución

Planteamos la ley de mallas y reemplazamos por los valores del ejercicio.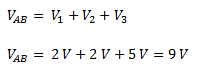

Ejercicio 6

Obtener las caídas de tensión en los resistores R₂ y R₃.

Datos V_R1 = 3 V, V_AB = 10 V

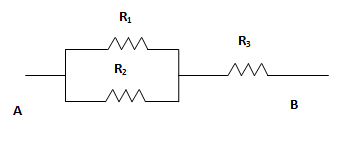
Solución

Por estar R₁ y R₂ en paralelo, la tensión es la misma para cada una de las dos resistencias.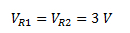



Reemplazamos R₁ y R₂ por una resistencia equivalente, cuya caída de tensión es igual a la de las resistencias individuales.



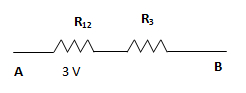
Planteamos la ley de mallas y despejamos V_R3.



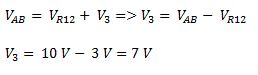
Seguir a ejercicios de potencia en corriente continua
Volver a ejercicios de corriente continua
Volver a home