
Ejercicios de ecuaciones diferenciales
Ejercicio 1
Comprobar que la función “y” es solución a la siguiente ecuación diferencial.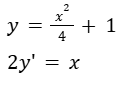
Respuesta
Calculamos la derivada de la función.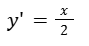
Reemplazamos la derivada en la ecuación diferencial.
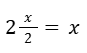
Simplificamos la expresión y vemos que se cumple la igualdad.
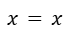
Ejercicio 2
Comprobar que la función “y” es solución a la siguiente ecuación diferencial.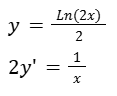
Respuesta
Calculamos la derivada de la función.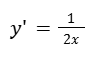
Reemplazamos la derivada en la ecuación diferencial.
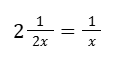
Simplificamos y vemos que se cumple la igualdad.
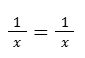
Ejercicio 3
Resolver la siguiente ecuación diferencial.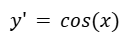
Respuesta
Escribimos la derivada con la notación de Leibniz.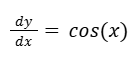
Vemos que es posible separar las variables.

Integramos de ambos lados.
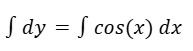
Resolvemos la integral. Como nos queda despejado “y” ya tenemos la solución.
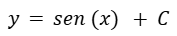
Ejercicio 4
Resolver la siguiente ecuación diferencial.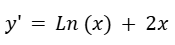
Respuesta
Escribimos la derivada con la notación de Leibniz.
Vemos que es posible separar las variables.
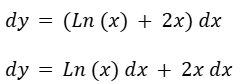
Integramos de ambos lados.
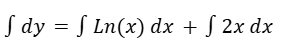
Resolvemos las integrales. Como nos queda despejado “y” ya tenemos la solución.
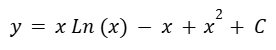
Ejercicio 5
Resolver la siguiente ecuación diferencial.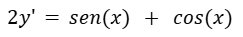
Respuesta
Escribimos la derivada con la notación de Leibniz.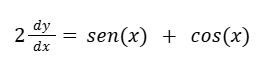
Vemos que es posible separar las variables.
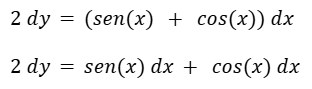
Integramos de ambos lados.
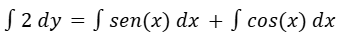
Resolvemos las integrales.
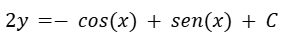
Despejamos “y” y obtenemos la solución.
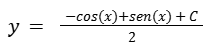
Ejercicio 6
Resolver la siguiente ecuación diferencial.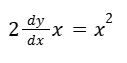
Respuesta
Vemos que es posible separar las variables.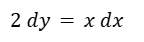
Integramos de ambos lados.
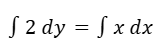
Resolvemos las integrales.

Despejamos “y” y obtenemos la solución.
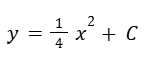
Volver a ecuaciones diferenciales
Volver a home