Ejercicios de clasificación de funciones
Ejercicio 1
Determinar si las siguientes funciones son inyectivas observando su gráfico.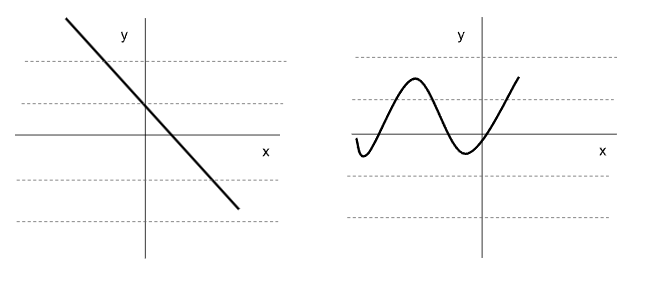
Respuesta
La primera función es inyectiva ya que no hay ninguna línea horizontal que corte al gráfico de la función más de una vez.La segunda función no es inyectiva ya que hay líneas horizontales que cortan al gráfico más de una vez.
Ejercicio 2
Dada la siguiente función: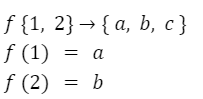
Determinar si es inyectiva.
Determinar si es sobreyectiva.
Determinar si es biyectiva.
Respuesta
La función es inyectiva ya que no hay ningún elemento de la imagen que provenga de más de un elemento del dominio.La función no es sobreyectiva ya que hay un elemento en la imagen que no proviene de ningún elemento del conjunto de salida.
La función no es biyectiva ya que no es sobreyectiva.
Ejercicio 3
Dada la siguiente función:
Determinar algebraicamente si es inyectiva.
Respuesta

La función no es inyectiva.
Ejercicio 4
Dadas las siguientes funciones: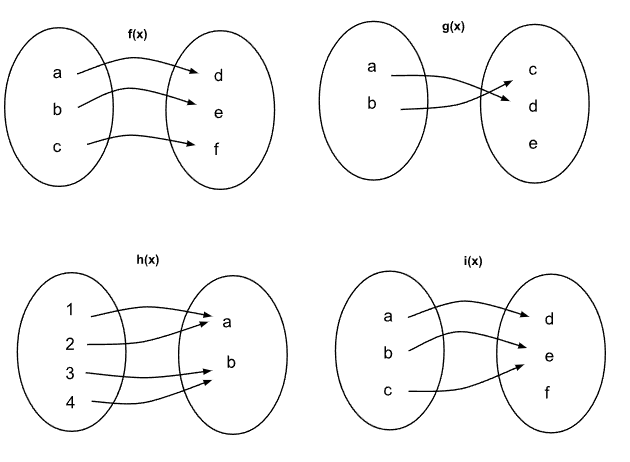
Determinar si son inyectivas.
Determinar si son sobreyectivas.
Determinar si son biyectivas.
Justificar las respuestas según las definiciones.
Respuesta
Para la función f(x):Es inyectiva ya que no hay ningún elemento en la imagen que provenga de más de una misma preimagen.
Es sobreyectiva ya que todos los elementos del conjunto de llegada tienen preimagen.
Es biyectiva porque es inyectiva y sobreyectiva.
Para la función g(x):
Es inyectiva ya que no hay ningún elemento en la imagen que provenga de más de un elemento del dominio.
No es sobreyectiva ya que el elemento “e” no tiene preimagen.
No es biyectiva ya que no es sobreyectiva.
Para la función h(x):
No es inyectiva ya que hay elementos en la imagen que provienen de más de una preimagen.
Es sobreyectiva porque todos los elementos de la imagen tienen una preimagen.
No es biyectiva ya que no es inyectiva.
Para la función i(x):
No inyectiva ya que el elemento “e” proviene de dos elementos diferentes del dominio.
No es sobreyectiva ya que el elemento “f” del conjunto de llegada no es imagen de ningún elemento del dominio.
No es biyectiva ya que no es inyectiva ni sobreyectiva.
Seguir a ejercicios de función lineal
Volver a ejercicios de funciones
Volver a home