Composición y descomposición de fuerzas
La composición y la descomposición de fuerzas son los procedimientos que consisten en transformar una fuerza en sus dos componentes rectangulares (descomposición) o sus dos componentes rectangulares en una fuerza (composición).Descomposición de fuerzas
La descomposición de fuerzas en componentes rectangulares consiste en hallar las proyecciones de una fuerza sobre sus dos ejes cartesianos. Es decir que se transforma una fuerza en otras dos que se encuentren sobre los ejes y que sumadas dan la fuerza original.Por ejemplo, una fuerza de 50 N con un ángulo de 30° la podemos representar de la siguiente manera:
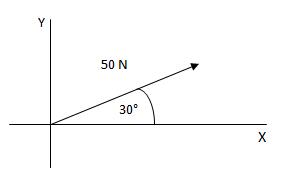
Lo que hacemos entonces es proyectar cada fuerza dada sobre los ejes X e Y, reemplazándola de esta manera por dos fuerzas perpendiculares entre sí que sumadas dan la fuerza original.
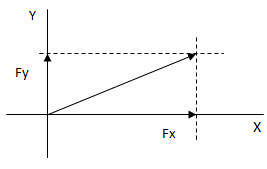
Debido a que entre las fuerzas y los ejes se forman triángulos rectángulos, descomponer una fuerza consiste en hallar dos catetos a partir del valor de la hipotenusa y de algún ángulo. Por lo tanto para llevar a cabo la descomposición se aplican relaciones trigonométricas.
En el ejemplo anterior tenemos a la componente FX como cateto adyacente al ángulo y a un cateto de igual longitud que la componente FY opuesto al ángulo. Por lo tanto:
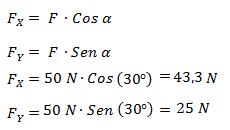
También podemos componer fuerzas. Es decir a partir de dos fuerzas hallar una sola. Es equivalente a tener dos catetos de un triángulo y buscar la hipotenusa. Esto se hace utilizando el teorema de Pitágoras (para hallar el largo) y relaciones trigonométricas para hallar el ángulo.
Ejemplo de descomposición con más de una fuerza
Si tenemos varias fuerzas podemos descomponer cada una sobre sus ejes y luego hacer una sumatoria por eje en el caso de que lo que queramos hacer sea sumarlas.En el siguiente ejemplo se tienen dos fuerzas y se calculan las dos componentes rectangulares para cada una.
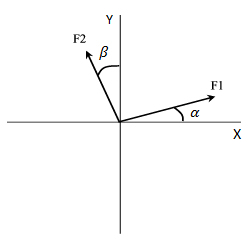
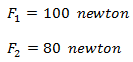
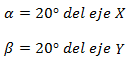
Proyectamos las fuerzas sobre los ejes
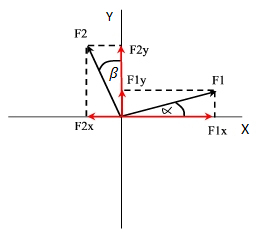
Para la F1
Planteamos las siguientes relaciones trigonométricas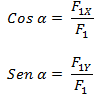
Despejamos las componentes sobre los ejes X e Y
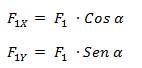
Para la F2
Planteamos las mismas relaciones trigonométricas para la fuerza número 2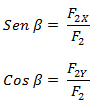
Despejamos las componentes sobre cada eje
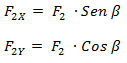
Luego de tener cada componente separada podemos hacer la sumatoria sobre cada eje y obtenemos una fuerza total FX para el eje X y otra FY para el eje Y.
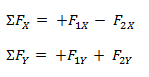
Composición de fuerzas
Para hallar la resultante total hay que realizar el procedimiento inverso, es decir componer las dos fuerzas.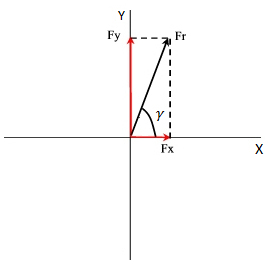
El módulo se calcula como la raíz cuadrada de cada componente al cuadrado:
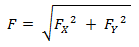
El ángulo se puede calcular con la tangente:
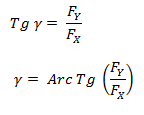
Suma de fuerzas
Volver a fuerza y tipos de fuerzas
Volver a home