
Características de la función cuadrática
Eje de simetría
Se denomina eje de simetría a un eje vertical (paralelo al eje “y”) sobre el cuál la parábola es simétrica hacia ambos lados.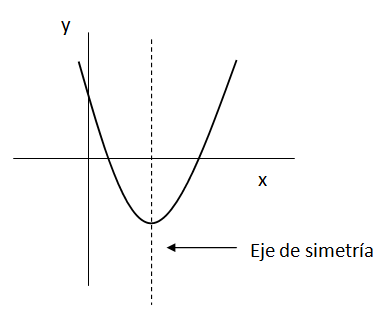
El valor de “x” por el cual pasa el eje de simetría se puede calcular con la siguiente fórmula.
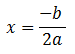
Vértice de la parábola
El vértice es el punto de la parábola en donde su valor es máximo o mínimo.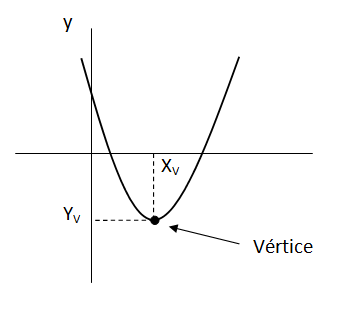
La componente “x” del vértice es el eje de simetría, mientras que la componente “y” la podemos obtener evaluando la parábola en el valor de “x” correspondiente al eje de simetría.
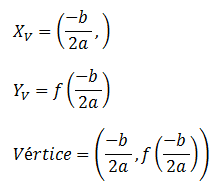
Raíces de una función cuadrática
Las raíces de una función cuadrática son los valores de “x” para los cuales la función (“y”) vale cero, es decir que también son los valores de “x” en los cuales la gráfica de la función corta al eje horizontal.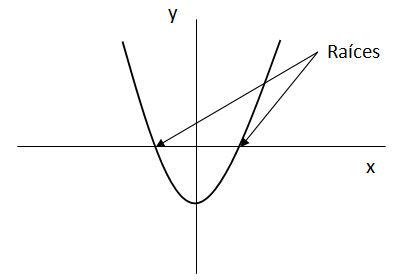
Para calcular las raíces igualamos la función a cero y luego aplicamos la siguiente fórmula, tanto con el signo positivo como con el signo negativo. De esta forma obtenemos las dos raíces.
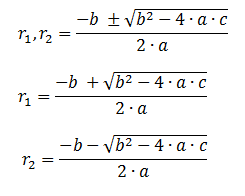
Una función cuadrática puede no tener raíces como en los siguientes ejemplos. En estos casos no podríamos calcular un valor con las fórmulas anteriores ya que obtendríamos un valor negativo dentro de la raíz cuadrada.
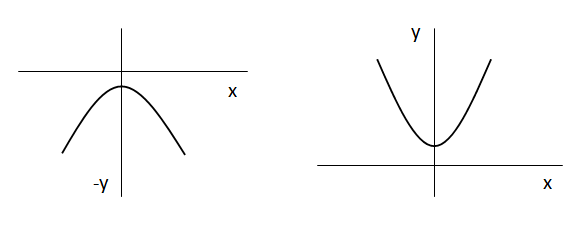
Seguir a gráfico de una función cuadrática
Volver a función cuadrática
Volver a home