Relación entre magnitudes angulares y tangenciales

Si tenemos las magnitudes angulares expresadas en radianes (por ejemplo la posición en radianes o la velocidad angular en radianes sobre segundos) podemos convertirlas fácilmente a magnitudes expresadas en función de la distancia recorrida sobre la circunferencia, multiplicándolas por el radio.

De la misma forma, si tenemos magnitudes expresadas en función de la distancia sobre la circunferencia podemos obtener las magnitudes angulares (en radianes) dividiéndolas por el radio.

Posición angular

Para convertir la posición angular (ángulo en el cual se encuentra el móvil desde el cero del sistema de referencia) hacia la distancia recorrida desde el cero sobre la circunferencia (en unidades de longitud) multiplicamos por el radio.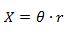



X = Distancia desde el cero [m]
θ = Ángulo desde el cero [rad]
r = Radio de giro [m]

De la misma forma si tenemos la posición sobre la circunferencia y queremos obtener la posición angular dividimos por el radio.



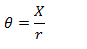
θ = Ángulo desde el cero [rad]
X = Distancia desde el cero [m]
r = Radio de giro [m]

Velocidad angular a tangencial

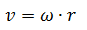
v = Velocidad tangencial [m/s]
ω = Velocidad angular [rad/s]
r = Radio de giro [m]

Aceleración angular a tangencial

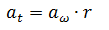
a_t = Aceleración tangencial [m/s²]
a_ω = Aceleración angular [rad/s²]
r = Radio de giro [m]


Seguir a ejercicios de MCU
Volver a mcu
Volver a home