
Conversión de números complejos
Es posible convertir fácilmente un número expresado en una forma al equivalente en la otra utilizando el teorema de Pitágoras y las funciones trigonométricas.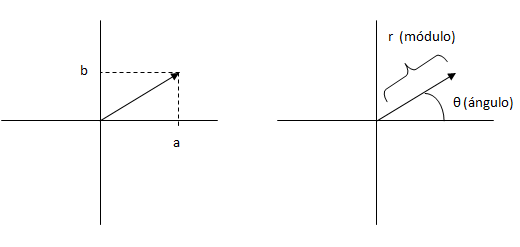
Forma binómica a forma polar
El módulo (que es la longitud de la hipotenusa de un triángulo) lo obtenemos como la raíz cuadrada de la suma de las dos componentes al cuadrado.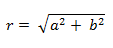
El ángulo lo obtenemos a través de funciones trigonométricas (típicamente se suele utilizar la inversa de la tangente). Si el número complejo pertenece al primer cuadrante lo podemos calcular de la siguiente manera:
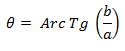
Si el número complejo no pertenece al primer cuadrante también podemos utilizar la función inversa de la tangente y luego sumar o restar ángulos para calcular el ángulo desde el primer cuadrante en sentido antihorario.
Forma polar a forma binómica
La conversión de forma polar a binómica consiste en hacer la proyección sobre cada eje. Esto se hace mediante las funciones trigonométricas seno y coseno.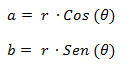
Volver a números complejos
Volver a home